网址:http://m.1010jiajiao.com/timu_id_12327[举报]
一.选择题(本大题共8小题,每小题5分,共40分)
(1)B (2)D (3)C (4)B
(5)D (6)D (7)A (8)C
二.填空题(本大题共6小题,每小题5分,共30分)
(9)(1,-1) (10){y|
y>1}, y = 2x-1 (x>1) (11)试卷.files\image128.gif) ,
,试卷.files\image130.gif)
(12)试卷.files\image132.gif) (13) 2 (14)R,
(13) 2 (14)R, 试卷.files\image134.gif) R
R
三.解答题(本大题共6小题,共80分)
15. 解(Ⅰ)恰有一名男生的概率为试卷.files\image136.gif) . ……………………………3分
. ……………………………3分
(Ⅱ)至少有一名男生的概率为试卷.files\image138.gif) . …………………………8分
. …………………………8分
(Ⅲ)至多有一名男生的概率为试卷.files\image138.gif) . …………………………13分
. …………………………13分
16. 解:(Ⅰ)试卷.files\image141.gif) . ……………………………3分
. ……………………………3分
又试卷.files\image143.gif) ,cosC=
,cosC=试卷.files\image145.gif) >0,
>0,
故在试卷.files\image097.gif) 中,
中,试卷.files\image147.gif) 、
、试卷.files\image149.gif) 是锐角. ∴
是锐角. ∴试卷.files\image151.gif) ,
,试卷.files\image153.gif) .
.
∴试卷.files\image155.gif) . ……………………7分
. ……………………7分
(Ⅱ) 试卷.files\image157.gif) .
……………………10分
.
……………………10分
由正弦定理 试卷.files\image159.gif) . 解得
. 解得试卷.files\image161.gif) ,c=6.
,c=6.
∴试卷.files\image163.gif) . ∴
. ∴试卷.files\image165.gif) ,即AC=5 . ……………………13分
,即AC=5 . ……………………13分
17. 解:(I)依条件得试卷.files\image167.gif) , …………………2分
, …………………2分
解得试卷.files\image169.gif) .
…………………………………………4分
.
…………………………………………4分
所以an=3+(n-1)=n+2. …………………………………………6分
(II)Pn=试卷.files\image171.gif) , b6=2×26-1=64,
, b6=2×26-1=64,
由试卷.files\image173.gif) >64得n2+5n-128>0.
………………………………9分
>64得n2+5n-128>0.
………………………………9分
所以n(n+5)>128.因为n是正整数,且n=9时,n(n+5)=126,
所以当n≥10时,n(n+5)>128. 即n≥10时,Pn> b6. ……………………………13分
18. (Ⅰ)解:∵正三棱柱中AC∥A
∴∠CAD是异面直线AD与A
连结CD,易知AD=CD=试卷.files\image175.gif) a,AC= a, 在△ACD中易求出cos∠CAD=
a,AC= a, 在△ACD中易求出cos∠CAD=试卷.files\image177.gif) .
.
因此异面直线AD与A试卷.files\image177.gif) . …………………………4分
. …………………………4分
试卷.files\image178.gif) (Ⅱ)解:设AC中点为G,连结GB,GD,
(Ⅱ)解:设AC中点为G,连结GB,GD,
∵△ABC是等边三角形, ∴GB⊥AC.
又DB⊥面ABC, ∴GD⊥AC.
∴∠DGB是所求二面角的平面角. …………………6分
依条件可求出GB=试卷.files\image180.gif) a.
a.
∴tan∠DGB=试卷.files\image182.gif) =
=试卷.files\image184.gif) .
.
∴∠DGB=arctan试卷.files\image184.gif) .
……………………………………………8分
.
……………………………………………8分
(Ⅲ)证明:
∵D是B1B的中点,∴△C1B1D≌△ABD. ∴AD= C1D. 于是△ADC1是等腰三角形.
∵E是AC1的中点, ∴DE⊥AC1. ………………………………………………10分
∵G是AC的中点,∴EG∥C试卷.files\image186.gif) C
C
∴四边形EGBD是平行四边形. ∴ED∥GB.
∵G是AC的中点,且AB=BC,∴GB⊥AC. ∴ED⊥AC.
∵AC∩AC1=A,
∴ED⊥平面ACC
(或证ED∥GB,GB⊥平面ACC
19. 解:(Ⅰ)∵试卷.files\image188.gif) ,
,
∴试卷.files\image190.gif) .
……………………………………3分
.
……………………………………3分
令试卷.files\image192.gif) 得,
得,试卷.files\image194.gif) =0
=0试卷.files\image196.gif) .
.
试卷.files\image198.gif) ,
,
∴试卷.files\image200.gif) 方程有两个不同的实根
方程有两个不同的实根试卷.files\image202.gif) 、
、试卷.files\image204.gif) .
.
令试卷.files\image206.gif) ,由
,由试卷.files\image208.gif) 可知:
可知:
当试卷.files\image210.gif) 时,
时,试卷.files\image212.gif) ;
;
当试卷.files\image214.gif) ;
;
当试卷.files\image216.gif) ;
;
∴试卷.files\image202.gif) 是极大值点,
是极大值点,试卷.files\image204.gif) 是极小值点. ……………………………………7分
是极小值点. ……………………………………7分
(Ⅱ)试卷.files\image218.gif) ,
,
所以得不等式试卷.files\image220.gif) .
.
即试卷.files\image222.gif) . ………10分
. ………10分
又由(Ⅰ)知试卷.files\image224.gif) ,
,
代入前面的不等式,两边除以(1+a),
并化简得试卷.files\image226.gif) ,解之得:
,解之得:试卷.files\image228.gif) ,或
,或试卷.files\image230.gif) (舍去).
(舍去).
所以当试卷.files\image228.gif) 时,不等式
时,不等式试卷.files\image116.gif) 成立.
…………………………14分
成立.
…………………………14分
20. 解:(Ⅰ)∵试卷.files\image234.gif)
∴试卷.files\image236.gif) .
………………………………………………2分
.
………………………………………………2分
又椭圆C经过点B(0,-1),解得b2=1.
所以a2=2+1=3. 故椭圆C的方程为试卷.files\image238.gif) . ……………………………4分
. ……………………………4分
(Ⅱ)设l的方程为:y= kx+m,M(x1,y1)、N(x2,y2),
试卷.files\image239.gif)
试卷.files\image241.gif) .
.
则x1+x2= -试卷.files\image243.gif) . ………………6分
. ………………6分
Δ=36 k
设线段MN的中点G(x0,y0),
x0=试卷.files\image245.gif) ,
,
线段MN的垂直平分线的方程为:y -试卷.files\image247.gif) .…………………8分
.…………………8分
∵|试卷.files\image249.gif) , ∴线段MN的垂直平分线过B(0,-1)点.
, ∴线段MN的垂直平分线过B(0,-1)点.
∴-1-试卷.files\image251.gif) . ∴m=
. ∴m=试卷.files\image253.gif) . ②
. ②
②代入①,得3k2 -(试卷.files\image255.gif) . ③
. ③
∵|试卷.files\image257.gif) 的夹角为60°,∴△BMN为等边三角形.
的夹角为60°,∴△BMN为等边三角形.
∴点B到直线MN的距离d=试卷.files\image259.gif) .
……………………………10分
.
……………………………10分
∵试卷.files\image261.gif) ,
,
又∵|MN|=试卷.files\image263.gif)
=试卷.files\image265.gif)
=试卷.files\image267.gif) ,
,
∴试卷.files\image269.gif) .
……………………………12分
.
……………………………12分
解得k2=试卷.files\image271.gif) ,满足③式. 代入②,得m=
,满足③式. 代入②,得m=试卷.files\image273.gif) .
.
直线l的方程为:y=试卷.files\image275.gif) .
……………………………14分
.
……………………………14分
 .
. 化简成
化简成 的形式(6分);
的形式(6分); ,求边AC的长. (7分);
,求边AC的长. (7分);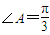 ,边
,边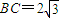 ,设∠B=x,△ABC的周长为y.
,设∠B=x,△ABC的周长为y.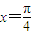 ,求边AC的长;
,求边AC的长;