摘要：1．位置关系:(1)两条异面直线相互垂直 证明方法:①证明两条异面直线所成角为90º,②证明线面垂直.得到线线垂直,③证明两条异面直线的方向量相互垂直.(2)直线和平面相互平行证明方法:①证明直线和这个平面内的一条直线相互平行,②证明这条直线的方向量和这个平面内的一个向量相互平行,③证明这条直线的方向量和这个平面的法向量相互垂直.(3)直线和平面垂直证明方法:①证明直线和平面内两条相交直线都垂直.②证明直线的方向量与这个平面内不共线的两个向量都垂直,③证明直线的方向量与这个平面的法向量相互平行.(4)平面和平面相互垂直证明方法:①证明这两个平面所成二面角的平面角为90º,②证明一个平面内的一条直线垂直于另外一个平面,③证明两个平面的法向量相互垂直.
网址：http://m.1010jiajiao.com/timu_id_120746[举报]
（2012•河南模拟）两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线l1：2x-y+a=0，l2：2x-y+a2+1=0和圆：x2+y2+2x-4=0相切，则a的取值范围是（ ）
两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线
，
和圆
相切，则
的取值范围是（ ）
A．
B．
或
C．
D．
查看习题详情和答案>>
两条平行直线和圆的位置关系定义为：若两条平行直线和圆有四个不同的公共点，则称两条平行线和圆“相交”；若两平行直线和圆没有公共点，则称两条平行线和圆“相离”；若两平行直线和圆有一个、两个或三个不同的公共点，则称两条平行线和圆“相切”．已知直线
相切，则a的取值范围是（ ）
A．
B．
C．-3≤a≤一
或≤a≤7 D．a≥7或a≤—3
查看习题详情和答案>>
相切，则a的取值范围是（ ）
或
≤a≤7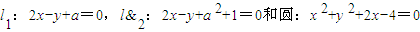
相切，则a的取值范围是（ ）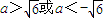
或
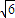≤a≤7