摘要：18．(1)设.由扩充的正弦定理.得 - 所以 -
网址：http://m.1010jiajiao.com/timu_id_11794[举报]
在坐标平面上有两个区域M和N，M为
对应的平面区域，N是随t变化的区域，它由不等式t≤x≤t+l所确定，t的取值范围是0≤t≤1，设M和N的公共面积是函数f（t），则f（t）=
查看习题详情和答案>>
|
-t2+t+
| 1 |
| 2 |
-t2+t+
．| 1 |
| 2 |
已知函数
．]
（1）求函数
的最小值和最小正周期；
（2）设
的内角
、
、
的对边分别为
，
，
，且
，
，
若
，求，的值．
【解析】第一问利用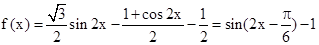
得打周期和最值
第二问
，由正弦定理，得
，①
由余弦定理，得
，即
，②
由①②解得
查看习题详情和答案>>
在坐标平面上有两个区域M和N，M为
对应的平面区域，N是随t变化的区域，它由不等式t≤x≤t+l所确定，t的取值范围是0≤t≤1，设M和N的公共面积是函数f（t），则f（t）= ．
查看习题详情和答案>>
对应的平面区域，N是随t变化的区域，它由不等式t≤x≤t+l所确定，t的取值范围是0≤t≤1，设M和N的公共面积是函数f（t），则f（t）= ．
查看习题详情和答案>>
对t∈R恒成立，求m的取值范围． 
，椭圆C：
，
、
分别为椭圆C的左、右焦点.
，0），所以
，得
.又因为m>1，所以
，故直线的方程为
，由
，消去x，得
，
，知
<8,且有
可知
从而
，设M是GH的中点，则M（
）.