摘要：解:(1)f(x)＝x3+ax2+bx+c.f¢(x)＝3x2+2ax+b由f¢()＝.f¢(1)＝3+2a+b＝0得a＝.b＝-2f¢(x)＝3x2-x-2＝.函数f(x)的单调区间如下表:x-(-.1)1f¢(x)+0-0+f(x)极大值¯极小值所以函数f(x)的递增区间是递减区间是(-.1)(2)f(x)＝x3-x2-2x+c.xÎ[-1.2].当x＝-时.f(x)＝+c为极大值.而f(2)＝2+c.则f(2)＝2+c为最大值.要使f(x)<c2恒成立.只需c2>f(2)＝2+c解得c<-1或c>2
网址：http://m.1010jiajiao.com/timu_id_11106[举报]
已知函数f（x）＝x3＋ax2＋bx＋c在x＝－
与x＝1时都取得极值
（1） 求a、b的值与函数f（x）的单调区间
（2） 若对xÎ〔－1，2〕，不等式f（x）<c2恒成立，求c的取值范围。
查看习题详情和答案>>（08年正定中学一模文）（12分）
已知函数f（x）＝x3＋ax2＋bx＋c在x＝－
与x＝1时都取得极值
（1） 求a、b的值与函数f（x）的单调区间
（2） 若对xÎ〔－1，2〕，不等式f（x）<c2恒成立，求c的取值范围。
查看习题详情和答案>>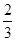
与x＝1时都取得极值.
与x＝1时都取得极值.
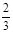与x＝1时都取得极值