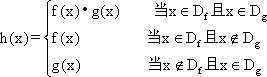摘要:解的定义域为.对f= e-ax. = e-2x, f '和均大于0, 所以f.为增函数.(?)当0<a<2时, f '在为增函数. (?)当a>2时, 0<<1, 令f '(x)=0 ,解得x1= - , x2= .当x变化时, f '的变化情况如下表: x(-,)(,1)f '(x)+-++f(x)ㄊㄋㄊㄊf, 在(-,)为减函数.
网址:http://m.1010jiajiao.com/timu_id_10977[举报]
已知定义域为R的单调函数f(x)是奇函数,当x>0时,![]() .
.
(1)求f(x)的解析式;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求实数k的取值范围.
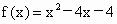 的定义域为[t-2,t-1],对任意tÎR,求函数f(x)的最小值j(t)的解析式.
的定义域为[t-2,t-1],对任意tÎR,求函数f(x)的最小值j(t)的解析式.
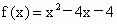 的定义域为[t-2,t-1],对任意tÎ
R,求函数f(x)的最小值j
(t)的解析式.
的定义域为[t-2,t-1],对任意tÎ
R,求函数f(x)的最小值j
(t)的解析式.