摘要：解: 椭圆方程可写为: + =1 式中a>b>0 , 且 得a2=4,b2=1,所以曲线C的方程为: x2+ =1 . y=2 y '=- 设P(x0,y0),因P在C上,有0<x0<1, y0=2, y '|x=x0= - ,得切线AB的方程为: y=- (x-x0)+y0 . 设A,由切线方程得 x= , y= .由= +得M的坐标为(x,y), 由x0,y0满足C的方程,得点M的轨迹方程为: + =1 (Ⅱ)| |2= x2+y2, y2= =4+ ,
网址：http://m.1010jiajiao.com/timu_id_10974[举报]
（2010•顺德区模拟）在直角坐标系xOy中，已知曲线C的参数方程是
（θ是参数），若以O为极点，x轴的正半轴为极轴，则曲线C的极坐标方程可写为
查看习题详情和答案>>
|
ρ=2sinθ
ρ=2sinθ
．
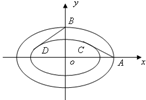简化的北京奥运会主体育场“鸟巢”的钢结构俯视图如图所示，内外两圈的钢骨架是离心率相同的椭圆，外层椭圆顶点向内层椭圆引切线AC，BD，设内层椭圆方程为| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| (ma)2 |
| y2 |
| (mb)2 |
| 9 |
| 16 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
有下列说法：
（1）0与{0}表示同一个集合；
（2）由1，2，3组成的集合可表示为{1，2，3}或{3，2，1}；
（3）方程（x-1）2（x-2）=0的所有解的集合可表示为{1，1，2}；
（4）集合{x|4＜x＜5}是有限集．
其中正确的说法是（ ）
（1）0与{0}表示同一个集合；
（2）由1，2，3组成的集合可表示为{1，2，3}或{3，2，1}；
（3）方程（x-1）2（x-2）=0的所有解的集合可表示为{1，1，2}；
（4）集合{x|4＜x＜5}是有限集．
其中正确的说法是（ ）
查看习题详情和答案>>