摘要:在“探究小车速度随时间变化规律的实验 中.打点计时器应接在 电源上.每隔 s打一次点.图3是某次实验的纸带.取中间一段. 从0点开始.每5个连续点取一个计数点.标以1.2.3--那么相邻两个计数点之间的时间为 s.各计数点与0计数点之间的距离依次为x=6cm.x=10.5cm.x=13.5cm.则物体打1计数点的速度= m/s.打2计数点的速度= m/s.运动的加速度为 m/s.
网址:http://m.1010jiajiao.com/timu_id_1090983[举报]
在“探究小车速度随时间变化规律”的实验中:
(1)下列操作正确的有
A、在释放小车前,小车要靠近打点计时器B、打点计时器应放在长木板的有滑轮一端C、应先接通电源,后释放小车D、电火花计时器应使用低压交流电源
(2)打点计时器原来使用的电源的频率是50Hz,若在测定匀变速直线运动的加速度时,
交流电的频率为60Hz而未被发觉,这样计算出的加速度值与真实值相比是
(3)某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示.在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为s1、s2和s3.由此可算出小车运动的加速度大小a=
,打点计时器在打C点时,小车的速度大小
.(用已知的物理量符号表示)

查看习题详情和答案>>
(1)下列操作正确的有
AC
AC
.(填选项代号)A、在释放小车前,小车要靠近打点计时器B、打点计时器应放在长木板的有滑轮一端C、应先接通电源,后释放小车D、电火花计时器应使用低压交流电源
(2)打点计时器原来使用的电源的频率是50Hz,若在测定匀变速直线运动的加速度时,
交流电的频率为60Hz而未被发觉,这样计算出的加速度值与真实值相比是
偏小
偏小
.(填“偏大”、“偏小”或“不变”)(3)某同学研究小车在斜面上的运动,用打点计时器记录了小车做匀变速直线运动的位移,得到一段纸带如图所示.在纸带上选取几个相邻计数点A、B、C、D,相邻计数点间的时间间隔均为T,B、C和D各点到A的距离为s1、s2和s3.由此可算出小车运动的加速度大小a=
| s3-s2-s1 |
| 2T2 |
| s3-s2-s1 |
| 2T2 |
| s3-s1 |
| 2T |
| s3-s1 |
| 2T |

在“探究小车速度随时间变化规律”的实验中,某同学测量数据后,通过计算得到了小车运动过程中各计时时刻的速度如表格所示.
①分析表中数据可知,在误差允许的范围内,小车做 运动.
②由于此次实验的原始纸带没有保存,另一同学想估算小车从位置0到位置5的位移,其估算方法如下:x=(0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1)m=…那么,该同学得到的位移 (选填“大于”、“等于”或“小于”)实际位移,为了使计算位移的误差尽可能小,你认为采取什么方法更合适?(不必算出具体数据) .
查看习题详情和答案>>
| 位置编号 | 0 | 1 | 2 | 3 | 4 | 5 |
| 时间t/s | O | 0.1 | 0.2 | O.3 | 0.4 | 0.5 |
| 速度v/m?s-1 | 0.38 | O.63 | 0.88 | 1.12 | 1.38 | 1.63 |
②由于此次实验的原始纸带没有保存,另一同学想估算小车从位置0到位置5的位移,其估算方法如下:x=(0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1)m=…那么,该同学得到的位移
在“探究小车速度随时间变化规律”的实验中:
(1)电火花计时器正常工作时,其打点的周期取决于
A.交流电压的高低
B.交流电的频率
C.墨粉纸盘的大小
D.纸带的长度
(2)下列操作中正确的有
A.在释放小车前,小车要靠近打点计时器
B.打点计时器应放在长木板的有滑轮一端
C.应先接通电源,后释放小车
D.电火花计时器应使用低压交流电源
(3)如图所示为同一打点计时器在四条水平运动的纸带上打出的点,四条纸带的a、b间的间距相等,则a、b间的平均速度最小的是
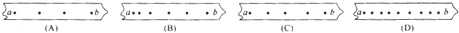
查看习题详情和答案>>
(1)电火花计时器正常工作时,其打点的周期取决于
B
B
.A.交流电压的高低
B.交流电的频率
C.墨粉纸盘的大小
D.纸带的长度
(2)下列操作中正确的有
AC
AC
.(填选项代号)A.在释放小车前,小车要靠近打点计时器
B.打点计时器应放在长木板的有滑轮一端
C.应先接通电源,后释放小车
D.电火花计时器应使用低压交流电源
(3)如图所示为同一打点计时器在四条水平运动的纸带上打出的点,四条纸带的a、b间的间距相等,则a、b间的平均速度最小的是
D
D
.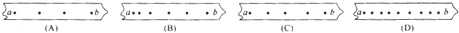
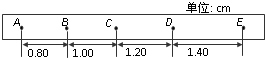 在“探究小车速度随时间变化规律”的实验中,打点计时器在纸带上依次打出一系列的点A,B,C,D,E,…,相邻两点间的距离如图所示,计时器打点周期为0.02s,则打c点时的瞬间,纸带的速度大小为
在“探究小车速度随时间变化规律”的实验中,打点计时器在纸带上依次打出一系列的点A,B,C,D,E,…,相邻两点间的距离如图所示,计时器打点周期为0.02s,则打c点时的瞬间,纸带的速度大小为0.55
0.55
m/s;纸带的加速度为5.0
5.0
m/s2.在“探究小车速度随时间变化规律”的实验中,某同学测量数据后,通过计算到了小车运动过程中各计时时刻的速度如表格所示:
因此次实验的原始纸带没有保存,另一同学想估算小车从位置0到位置5的位移,其所用方法是将每个0.1s视为匀速运动,然后估算如下:
x=(0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1)那么,该同学得到的位移
查看习题详情和答案>>
| 位置编号 | 0 | 1 | 2 | 3 | 4 | 5 |
| 时间t/s | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| 速度v/m?s-1 | 0.38 | 0.63 | 0.88 | 1.12 | 1.38 | 1.63 |
x=(0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1)那么,该同学得到的位移
小于
小于
.(选填“大于”、“等于”或“小于”)实际位移,为了使计算位移的误差尽可能小,你认为采取什么方法更合适,为什么?(不必算出具体数据)可以先计算相邻位置间的平均速度,再得到位移,这是因为表中每隔0.1s的速度增加在误差范围内相同,即为匀变速直线运动,平均速度可以由公式
=
求出,还可以求出加速度,应用匀变速直线运动公式x=v0t+
at2得出位移.
. |
| v |
| v1+v2 |
| 2 |
| 1 |
| 2 |
可以先计算相邻位置间的平均速度,再得到位移,这是因为表中每隔0.1s的速度增加在误差范围内相同,即为匀变速直线运动,平均速度可以由公式
=
求出,还可以求出加速度,应用匀变速直线运动公式x=v0t+
at2得出位移.
.. |
| v |
| v1+v2 |
| 2 |
| 1 |
| 2 |