摘要：(15)设.函数有最大值.∵有最小值.∴ 0<a<1. 则不等式的解为.解得2<x<3.所以不等式的解集为.
网址：http://m.1010jiajiao.com/timu_id_10795[举报]
设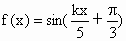
，其中k≠0．
(1)写出f(x)的最大值M、最小值m与最小正周期；
(2)求最小的正整数k，使得当自变量x在任意两个整数之间(包括整数本身)变化时，函数f(x)至少有一个值是M与一个值是m．
查看习题详情和答案>>设
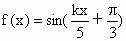，其中k≠0．
(1)
写出f(x)的最大值M、最小值m与最小正周期；(2)
求最小的正整数k，使得当自变量x在任意两个整数之间(包括整数本身)变化时，函数f(x)至少有一个值是M与一个值是m． 查看习题详情和答案>>设函数y=f（x）在（a，b）上的导函数为f′（x），f′（x）在（a，b）上的导函数为f″（x），若在a，b）上，f″（x）＜0恒成立，则称函数函数f（x）在（a，b）上为“凸函数”．已知当m≤2时，f(x)=
x3-
mx2+x在（-1，2）上是“凸函数”．则f（x）在（-1，2）上（ ）
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值，也有极小值 |
| B、既有极大值，也有最小值 |
| C、有极大值，没有极小值 |
| D、没有极大值，也没有极小值 |