摘要:1.本题共4小题.第1.第2.第3小题每小题3分.第4小题5分. 杨辉是中国南宋末年的一位杰出的数学家.数学教育家.杨辉三角是杨辉的一大重要研究成果.它的许多性质与组合数的性质有关.杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角: (1)求第20行中从左到右的第4个数, (2)若第n行中从左到右第14与第15个数 的比为.求n的值, 杨辉三角的所有数 的和, (4)在第3斜列中.前5个数依次为1.3. 6.10.15,第4斜列中.第5个数为35. 显然.1+3+6+10+15=35.事实上.一般地 有这样的结论:第m斜列中(从右上到左 下)前k个数之和.一定等于第m+1斜列中第k个数.试用含有m.k的数学公式表示上述结论.并给予证明.
网址:http://m.1010jiajiao.com/timu3_id_535488[举报]
(本大题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
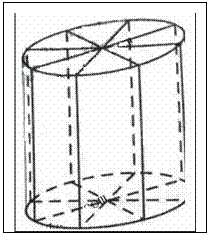 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用![]() 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径![]() 取何值时,
取何值时,![]() 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出
用于灯笼的三视图(作图时,不需考虑骨架等因素).
查看习题详情和答案>>(本大题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用![]() 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径![]() 取何值时,
取何值时,![]() 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出
用于灯笼的三视图(作图时,不需考虑骨架等因素).
查看习题详情和答案>>(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
(理科)已知四棱锥 的底面
的底面 是直角梯形,
是直角梯形,  ,
, ,
,
侧面 为正三角形,
为正三角形, ,
, .如图4所示.
.如图4所示.

(1) 证明:  平面
平面 ;
;
(2) 求四棱锥 的体积
的体积 .
.
查看习题详情和答案>>
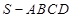 的底面
的底面 是直角梯形,
是直角梯形,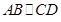 ,
,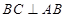 ,
,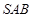 为正三角形,
为正三角形,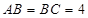 ,
,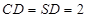 .如图4所示.
.如图4所示.
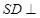 平面
平面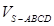 .
.