摘要: 直角坐标系下.O为坐标原点.定点E(0.4).动点满足 (Ⅰ)求动点的轨迹C的方程, (Ⅱ)设点A(0.).过A点的直线交(Ⅰ)中曲线于P.Q两点.Q点关于轴对称点为R (1)求证:点P.R.B三点共线, (2)若求点B到直线的距离的取值范围 哈师大附中2009年高三第四次模拟考试
网址:http://m.1010jiajiao.com/timu3_id_534565[举报]
直角坐标系下,O为坐标原点,定点E(0,4),动点M(x,y)满足
•
=y2
(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)过曲线C上任意一点M(x0,y0)(x0≠0)做两条倾斜角互补的弦MA、MB,其中A、B在曲线C上,证明:曲线C在点M处切线的斜率与弦AB的斜率之和为0.
查看习题详情和答案>>
| MO |
| ME |
(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)过曲线C上任意一点M(x0,y0)(x0≠0)做两条倾斜角互补的弦MA、MB,其中A、B在曲线C上,证明:曲线C在点M处切线的斜率与弦AB的斜率之和为0.
直角坐标系下,O为坐标原点,定点E(8,0),动点M(x,y)满足
•
=x2,
(1)求动点M(x,y)的轨迹C的方程;
(2)过定点F(2,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值;
(3)定点P(2,4),动点A,B是轨迹C上的三个点,且满足KPA•KPB=8试问AB所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由. 查看习题详情和答案>>
| MO |
| ME |
(1)求动点M(x,y)的轨迹C的方程;
(2)过定点F(2,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值;
(3)定点P(2,4),动点A,B是轨迹C上的三个点,且满足KPA•KPB=8试问AB所在的直线是否过定点,若是,求出该定点的坐标;否则说明理由. 查看习题详情和答案>>
(2009•台州二模)直角坐标系下,O为坐标原点,定点E(4,0),动点M(x,y)满足
•
=x2.
(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)过定点F(1,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值.
查看习题详情和答案>>
| MO |
| ME |
(Ⅰ)求动点M(x,y)的轨迹C的方程;
(Ⅱ)过定点F(1,0)作互相垂直的直线l1,l2分别交轨迹C于点M,N和点R,Q,求四边形MRNQ面积的最小值.
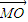 •
•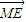 =x2,
=x2,