摘要: 在平面直角坐标系中.已知两点.若某直线上有且只有一点.使 .则称直线为“黄金直线 .点P为“黄金点 . (1) 当时.点能否成为“黄金点 .若能.求出“黄金直线 方程,若不能.请说明理由. (2)当满足什么条件时, “黄金点 P的轨迹是圆?此时的“黄金直线 具有什么特征? 19 (1)已知.试求函数的最小值, (2)若.求证:(Ⅰ). (Ⅱ)
网址:http://m.1010jiajiao.com/timu3_id_533984[举报]
.(本小题满分16分)
平面直角坐标系xOy中,已知圆M经过F1(0,-c),F2(0,c),A(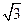 c,0)三点,其中c>0
c,0)三点,其中c>0
(1)求圆M的标准方程(用含c的式子表示);
(2)已知椭圆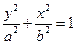
 (其中
(其中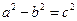 )的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
)的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
求椭圆离心率的取值范围;
若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由。
平面直角坐标系xOy中,已知圆M经过F1(0,-c),F2(0,c),A(
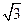 c,0)三点,其中c>0
c,0)三点,其中c>0(1)求圆M的标准方程(用含c的式子表示);
(2)已知椭圆
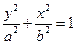
 (其中
(其中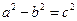 )的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。
)的左、右顶点分别为D、B,圆 M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧。求椭圆离心率的取值范围;
若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由。
(本小题满分16分)
已知在直角坐标系中,![]() ,其中数列
,其中数列![]() 都是递增数列。
都是递增数列。
(1)若![]() ,判断直线
,判断直线![]() 与
与![]() 是否平行;
是否平行;
(2)若数列![]() 都是正项等差数列,设四边形
都是正项等差数列,设四边形![]() 的面积为
的面积为![]() .
.
求证:![]() 也是等差数列;
也是等差数列;
(3)若![]() ,
,![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,数列
,数列![]() 前8项依次递减,求满足条件的数列
前8项依次递减,求满足条件的数列![]() 的个数。
的个数。
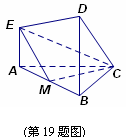 ⑴求证:
⑴求证: 中,已知点
中,已知点 为椭圆
为椭圆 的右顶点, 点
的右顶点, 点 ,点
,点 在椭
在椭 .
.
 的方程;
的方程; 三点的圆
三点的圆 截得的弦长;
截得的弦长; 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.