摘要:37.(命题人:南通中学赵栋.审题人:南通中学杨建楠.原创) 设定义在上的函数的图象为C.C的端点为点A.B.M是C上的任意一点.向量...若.记向量.现在定义“函数在上可在标准k下线性近似 是指恒成立.其中k是一个人为确定的正数. (1)证明:, (2)请你给出一个标准k的范围.使得[0.1]上的函数y=x2与y=x3中有且只有一个可在标准k下线性近似. [解析](1)由题意.x1≤x≤x2.即x1≤x1+(1-)x2≤x2.∴ x1- x2≤(x1-x2)≤0. ∵ x1- x2<0.∴ 0≤≤1. (2)由=+(1-).得=. 所以B.N.A三点在一条直线上. 又由(1)的结论.N在线段AB上.且与点M的横坐标相同. 对于 [0.1]上的函数y=x2.A. 则有||= x -x2 =.故. 对于[0.1]上的函数y=x3.则有= x-x3= g(x). 在(0.1)上. g′(x)= 1-3 x2. 可知在(0.1)上y= g(x)只有一个极大值点x=. 所以函数y= g(x)在(0.)上是增函数;在(.1)上是减函数. 又g()=.故[0.]. 经过比较.<.所以取k[.).则有函数y=x2在[0.1]上可在标准k下线性近似.函数y=x3在[0.1]上不可在标准k下线性近似.
网址:http://m.1010jiajiao.com/timu3_id_533659[举报]
设定义在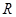 上的函数
上的函数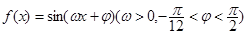 ,给出以下四个论断:
,给出以下四个论断:
①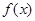 的周期为π;
②
的周期为π;
②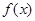 在区间(
在区间(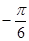 ,0)上是增函数;
,0)上是增函数;
③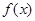 的图象关于点(
的图象关于点(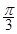 ,0)对称;④
,0)对称;④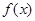 的图象关于直线
的图象关于直线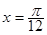 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题(写成“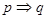 ”的形式): (其中用到的论断都用序号表示)
”的形式): (其中用到的论断都用序号表示)
查看习题详情和答案>>
(14分)已知函数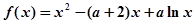 ,其中常数
,其中常数 。
。
(1)当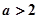 时,求函数
时,求函数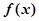 的单调递增区间;
的单调递增区间;
(2)当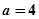 时,是否存在实数
时,是否存在实数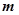 ,使得直线
,使得直线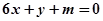 恰为曲线
恰为曲线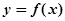 的切线?若存在,求出
的切线?若存在,求出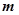 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(3)设定义在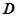 上的函数
上的函数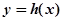 的图象在点
的图象在点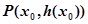 处的切线方程为
处的切线方程为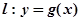 ,当
,当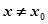 时,若
时,若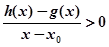 在
在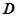 内恒成立,则称
内恒成立,则称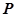 为函数
为函数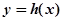 的“类对称点”。当
的“类对称点”。当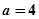 ,试问
,试问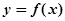 是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
是否存在“类对称点”?若存在,请至少求出一个“类对称点”的横坐标;若不存在,说明理由.
查看习题详情和答案>>
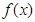 是定义在
是定义在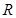 上以
上以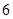 为周期的函数,
为周期的函数,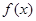 在
在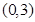 内单调递减,且
内单调递减,且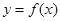 的图象关于直线
的图象关于直线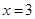 对称,则下面正确的结论是(
)
对称,则下面正确的结论是(
)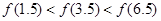 B.
B.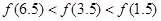
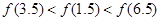 D.
D.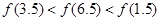
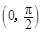 上的函数
上的函数 的图象与
的图象与 图象的交点横坐标为
图象的交点横坐标为 ,则
,则