摘要： (Ⅰ)由三视图可知:底面.底面ABCD为直角梯形.PB=BC=CD=1.AB=2.∴ . ----3分 (Ⅱ)当M为PB的中点时.CM∥平面PDA. 取PA中点N.连结MN.DN.可证MN∥CD.且MN＝CD.∴CM∥DN.故CM∥平面PDA. ----6分 (Ⅲ)分别以BC.BA.BP所在直线为x轴.y轴.z轴.建立空间直角坐标系. 则. 假设在BC边上存在点Q.使得二面角A-PD-Q为.设.平面的法向量为.则由.及.得..得. 同理.设平面的法向量为.可得,∴ .解得.∴.故存在点Q为BC的中点.使二面角A-PD-Q为.---12分
网址：http://m.1010jiajiao.com/timu3_id_533396[举报]
如图，网格纸上小正方形的边长为
，粗线画出的是某几何体的三视图，则此几何体的体积为（ ）
【解析】选
由三视图可知，该几何体是三棱锥，底面是俯视图，高为
，所以几何体的体积为
,选B.
查看习题详情和答案>>
图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则截面图形可能是( )
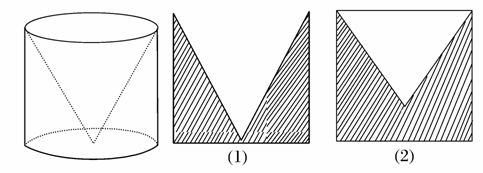
A．(1)(2) B．(1)(3)
C．(1)(4) D．(1)(5)
查看习题详情和答案>>图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则截面图形可能是 ( )
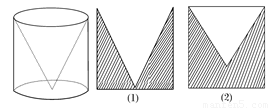
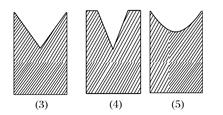
A．(1)(2) B．(1)(3) C．(1)(4) D．(1)(5)
查看习题详情和答案>>
图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则截面图形可能是 ( )
| A．(1)(2) | B．(1)(3) | C．(1)(4) | D．(1)(5) |
