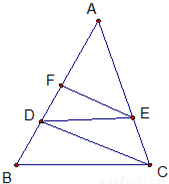
解:(1)∵EF∥CD∥AB.EG∥PB.根据面面平行的判定定理 ∴平面EFG∥平面PAB.又PA面PAB.∴AP∥平面EFG --------4分 (2)∵平面PDC⊥平面ABCD.AD⊥DC ——青夏教育精英家教网——

摘要：解:(1)∵EF∥CD∥AB.EG∥PB.根据面面平行的判定定理 ∴平面EFG∥平面PAB.又PA面PAB.∴AP∥平面EFG --------4分 (2)∵平面PDC⊥平面ABCD.AD⊥DC ∴AD⊥平面PCD.而BC∥AD. ∴BC⊥面EFD 过C作CR⊥EF交EF延长线于R点连GR.根据三垂线定理知∠GRC即为二面角的平面角.∵GC=CR.∴∠GRC=45°.---8分故二面角G-EF-D的大小为45°. -------9分 (3)Q点为PB的中点.取PC中点M.则QM∥BC.∴QM⊥PC 在等腰Rt△PDC中.DM⊥PC.∴PC⊥面ADMQ --------13分

网址：http://m.1010jiajiao.com/timu3_id_533325[举报]

用向量证明：梯形中位线平行于底且等于上、下两底和的一半.已知：如图2-2-20，梯形ABCD中，E、F是两腰AD、BC的中点，求证：EF∥CD∥AB且EF=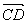（AB+CD）.

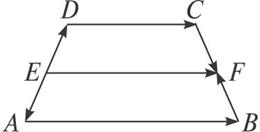
图2-2-20

查看习题详情和答案>>

用向量证明：梯形中位线平行于两底且等于上、下两底和的一半．

已知：如图，梯形ABCD中，E、F是两腰AD、BC的中点，求证：EF∥CD∥AB且EF＝(AB＋CD)．

查看习题详情和答案>>

用向量证明：梯形中位线平行于底且等于上、下两底和的一半.已知：如图2-2-20，梯形ABCD中，E、F是两腰AD、BC的中点，求证：EF∥CD∥AB且EF=

图2-2-20

查看习题详情和答案>>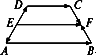

（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（不等式选做题）．不等式：|x-1|+|x+2|＜5的解集是

．
B．（几何证明选做题）如图，在△ABC中，DE∥BC，EF∥CD，若BC=3，DE=2，DF=1，则AB的长为

．
C．（坐标系与参数方程选做题）在已知极坐标系中，已知圆ρ=2cosθ与直线 3ρcosθ+4ρsinθ+a=0相切，则实数a=

查看习题详情和答案>>

（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评阅记分）
A．（不等式选做题）．不等式：|x-1|+|x+2|＜5的解集是    ．
B．（几何证明选做题）如图，在△ABC中，DE∥BC，EF∥CD，若BC=3，DE=2，DF=1，则AB的长为    ．
C．（坐标系与参数方程选做题）在已知极坐标系中，已知圆ρ=2cosθ与直线 3ρcosθ+4ρsinθ+a=0相切，则实数a=    ．

查看习题详情和答案>>