摘要: 某校从参加高二年级学业水平测试的学生中抽出80名学生.其数学成绩的频率分布直方图如图所示. (1)估计这次测试数学成绩的平均分; (2)假设在[90,100]段的学生的数学成绩都不相同.且都在94分以上.现用简单随机抽样的方法.从95,96,97,98,99,100这6个数中任取2个数.求这两个数恰好是在[90.100]段的两个学生的数学成绩的概率 已知等差数列的前项和为.公差成等比数列. (Ⅰ)求数列的通项公式, (Ⅱ)若从数列中依次取出第2项.第4项.第8项.--..--.按原来顺序组成一个新数列.记该数列的前项和为.求的表达式. 已知定义在上的函数在区间上的最大值是5.最小值是-11. (Ⅰ)求函数的解析式, (Ⅱ)若时.恒成立.求实数的取值范围. 已知直线所经过的定点恰好是椭圆的一个焦点,且椭圆上的点到点的最大距离为8. (Ⅰ)求椭圆的标准方程, (Ⅱ)已知圆,直线.试证明:当点在椭圆上运动时.直线与圆恒相交.并求直线被圆所截得弦长的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_532741[举报]
(本小题满分12分)

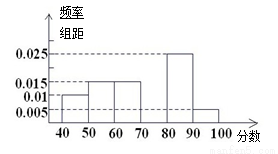
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次测试数学成绩的平均分;
(Ⅱ)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率.
查看习题详情和答案>>
(本小题满分12分)

某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次测试数学成绩的平均分;
(Ⅱ)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率.

某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次测试数学成绩的平均分;
(Ⅱ)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率.
(本小题满分12分)
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | 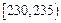 | 8 | 0.16 |
| 第二组 | 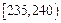 | ① | 0.24 |
| 第三组 | 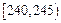 | 15 | ② |
| 第四组 | 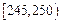 | 10 | 0.20 |
| 第五组 | 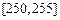 | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率. 查看习题详情和答案>>
(本小题满分12分)
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |
| 8 | 0.16 |
| 第二组 |
| ① | 0.24 |
| 第三组 |
| 15 | ② |
| 第四组 |
| 10 | 0.20 |
| 第五组 |
| 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
查看习题详情和答案>>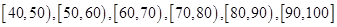 后,画出如下部分频率分布直方图。观察图形,回答下列问题:
后,画出如下部分频率分布直方图。观察图形,回答下列问题: