摘要: (本题满分18分.第1小题4分.第2小题5分.第3小题9分) 如图.已知点.动点在轴上.点 在轴上.其横坐标不小于零.点在直线上. 且满足.. (1)当点在轴上移动时.求点的轨迹, (2)过定点作互相垂直的直线与.与 (1)中的轨迹交于.两点.与(1)中的轨迹交于.两点.求四边形面积的最小值, 中的曲线推广为椭圆:.并将(2)中的定点取为焦点 .求与(2)相类似的问题的解.
网址:http://m.1010jiajiao.com/timu3_id_532312[举报]
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足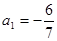 ,
,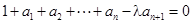 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),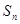 为数列{an}的前
为数列{an}的前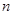 项和.
项和.
(1) 若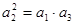 ,求
,求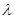 的值;
的值;
(2) 求数列{an}的通项公式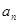 ;
;
(3) 当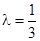 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
查看习题详情和答案>>
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足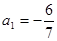 ,
, (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),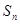 为数列{an}的前
为数列{an}的前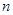 项和.
项和.
(1) 若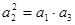 ,求
,求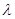 的值;
的值;
(2) 求数列{an}的通项公式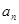 ;
;
(3) 当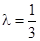 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
(本题满分18分,第1小题4分,第2小题6分,第3小题8分)
已知数列{an}满足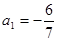 ,
,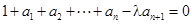 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),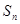 为数列{an}的前
为数列{an}的前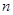 项和.
项和.
(1) 若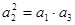 ,求
,求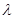 的值;
的值;
(2) 求数列{an}的通项公式 ;
;
(3) 当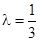 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
已知数列{an}满足
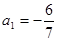 ,
,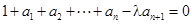 (其中λ≠0且λ≠–1,n∈N*),
(其中λ≠0且λ≠–1,n∈N*),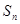 为数列{an}的前
为数列{an}的前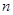 项和.
项和.(1) 若
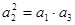 ,求
,求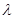 的值;
的值;(2) 求数列{an}的通项公式
 ;
;(3) 当
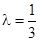 时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.
时,数列{an}中是否存在三项构成等差数列,若存在,请求出此三项;若不存在,请说明理由.