摘要: 已知函数.设.(Ⅰ)求F(x)的单调区间, (Ⅱ)若以图象上任意一点为切点的切线的斜率 恒成立.求实数的最小值
网址:http://m.1010jiajiao.com/timu3_id_531886[举报]
已知函数![]() ,设
,设![]() 。
。
(1)求F(x)的单调区间;
(2)若以![]() 图象上任意一点
图象上任意一点![]() 为切点的切线的斜率
为切点的切线的斜率![]() 恒成立,求实数
恒成立,求实数![]() 的最小值。
的最小值。
(3)是否存在实数![]() ,使得函数
,使得函数![]() 的图象与
的图象与![]() 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出![]() 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
已知函数 ,
, ,k为非零实数.
,k为非零实数.
(Ⅰ)设t=k2,若函数f(x),g(x)在区间(0,+∞)上单调性相同,求k的取值范围;
(Ⅱ)是否存在正实数k,都能找到t∈[1,2],使得关于x的方程f(x)=g(x)在[1,5]上有且仅有一个实数根,且在[-5,-1]上至多有一个实数根.若存在,请求出所有k的值的集合;若不存在,请说明理由.
【解析】本试题考查了运用导数来研究函数的单调性,并求解参数的取值范围。与此同时还能对于方程解的问题,转化为图像与图像的交点问题来长处理的数学思想的运用。
查看习题详情和答案>>
已知函数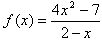 ,x∈[0,1],
,x∈[0,1],
(1)求f(x)的单调区间和值域;
(2)设a≥1,函数g(x)=x3-3ax-2a,x∈[0,1],若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围。
查看习题详情和答案>>
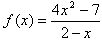 ,x∈[0,1],
,x∈[0,1],(1)求f(x)的单调区间和值域;
(2)设a≥1,函数g(x)=x3-3ax-2a,x∈[0,1],若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围。
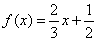 ,
,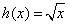 。
。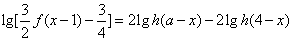 ;
;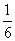 。
。 ,
, 。
。 ;
; 与
与 的大小。
的大小。