摘要：(1)证明:取B1C1的中点Q.连结A1Q.PQ.∴B1C1⊥A1Q.B1C1⊥PQ.∴B1C1⊥平面AP1Q. ∴B1C1⊥PA1. ∵BC∥B1C1.∴BC⊥PA1. (2)连结BQ.在△PB1C1中.PB1=PC1=.B1C1=2.Q为中点. ∴PQ=1.∴BB1=PQ.∴BB1∥PQ.∴四边形BB1PQ为平行四边形. ∴PB1∥BQ. ∴BQ∥DC1.∴PB1∥DC1.又∵PB1面AC1D.. ∴PB1∥平面AC1D.(3)=
网址：http://m.1010jiajiao.com/timu3_id_531813[举报]
（2013•四川）如图，在三棱柱ABC-A1B1C中，侧棱AA1⊥底面ABC，AB=AC=2AA1=2，∠BAC=120°，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．（Ⅰ）在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；
（Ⅱ）设（Ⅰ）中的直线l交AC于点Q，求三棱锥A1-QC1D的体积．（锥体体积公式：V=
| 1 | 3 |
（12分）如图，在三棱柱ABC﹣A1B1C中，侧棱AA1⊥底面ABC，AB=AC=2AA1=2，∠BAC=120°，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．
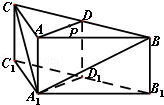
（Ⅰ）在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；
（Ⅱ）设（Ⅰ）中的直线l交AC于点Q，求三棱锥A1﹣QC1D的体积．（锥体体积公式：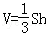
，其中S为底面面积，h为高）
查看习题详情和答案>>
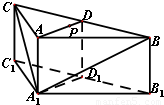如图，在三棱柱ABC-A1B1C中，侧棱AA1⊥底面ABC，AB=AC=2AA1=2，∠BAC=120°，D，D1分别是线段BC，B1C1的中点，P是线段AD上异于端点的点．（Ⅰ）在平面ABC内，试作出过点P与平面A1BC平行的直线l，说明理由，并证明直线l⊥平面ADD1A1；
（Ⅱ）设（Ⅰ）中的直线l交AC于点Q，求三棱锥A1-QC1D的体积．（锥体体积公式：
，其中S为底面面积，h为高）查看习题详情和答案>>
Sh，其中S为底面面积，h为高)
如图，在正方体ABCD-A1B1C1D1中，点E、F分别是AB、C1D1的中点．