摘要：20．已知函数.． (1)证明:当时., (2)若不等式对任意的.时恒成立.求实数的取值范围．
网址：http://m.1010jiajiao.com/timu3_id_531425[举报]
已知函数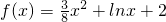
，g（x）=x．
（Ⅰ）求函数F（x）=f（x）-2•g（x）的极值点；
（Ⅱ）若函数F（x）=f（x）-2•g（x）在[et，+∞）（t∈Z）上有零点，求t的最大值；
（Ⅲ）证明：当x＞0时，有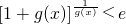
成立；若
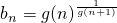（n∈N*），试问数列{bn}中是否存在bn=bm（n≠m）？若存在，求出所有相等的两项；若不存在，请说明理由．（e为自然对数的底数）
查看习题详情和答案>>
已知函数
，
为函数
的导函数．
（1）若数列
满足：
，
（
），求数列的通项
；
（2）若数列
满足：
，
（）．
①当
时，数列是否为等差数列？若是，请求出数列的通项
；若不是，请说明理由；
②当
时， 求证：
．
已知函数
，g（x）=x．
（Ⅰ）求函数F（x）=f（x）-2•g（x）的极值点；
（Ⅱ）若函数F（x）=f（x）-2•g（x）在[et，+∞）（t∈Z）上有零点，求t的最大值；
（Ⅲ）证明：当x＞0时，有
成立；若
（n∈N*），试问数列{bn}中是否存在bn=bm（n≠m）？若存在，求出所有相等的两项；若不存在，请说明理由．（e为自然对数的底数）
查看习题详情和答案>>
，g（x）=x．（Ⅰ）求函数F（x）=f（x）-2•g（x）的极值点；
（Ⅱ）若函数F（x）=f（x）-2•g（x）在[et，+∞）（t∈Z）上有零点，求t的最大值；
（Ⅲ）证明：当x＞0时，有
成立；若（n∈N*），试问数列{bn}中是否存在bn=bm（n≠m）？若存在，求出所有相等的两项；若不存在，请说明理由．（e为自然对数的底数）查看习题详情和答案>>
，g（x）=x．
成立；若
（n∈N*），试问数列{bn}中是否存在bn=bm（n≠m）？若存在，求出所有相等的两项；若不存在，请说明理由．（e为自然对数的底数）