摘要:22.B.选修4-4:坐标系与参数方程 已知圆系的方程为x2+y2-2axCos-2aySin=0 (1) 求圆系圆心的轨迹方程; (2) 证明圆心轨迹与动圆相交所得的公共弦长为定值;
网址:http://m.1010jiajiao.com/timu3_id_529810[举报]
(本小题满分10分)选修4-1《几何证明选讲》.
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点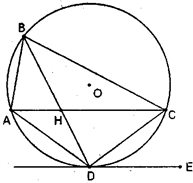
(Ⅰ)求证:BD平分∠ABC
(Ⅱ)若AB=4,AD=6,BD=8,求AH的长.
(本小题满分10分)选修4-4:坐标系与参数方程已知曲线C的极坐标方程是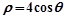 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
( 是参数).
是参数).
(1)将曲线C的极坐标方程和直线 参数方程转化为普通方程;
参数方程转化为普通方程;
(2)若直线l与曲线C相交于A、B两点,且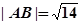 ,试求实数
,试求实数 值.
值.
查看习题详情和答案>>
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是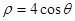 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: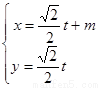 (
(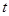 是参数).
是参数).
(I)将曲线C的极坐标方程和直线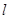 参数方程转化为普通方程;
参数方程转化为普通方程;
(II)若直线l与曲线C相交于A、B两点,且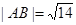 ,试求实数
,试求实数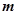 值.
值.
查看习题详情和答案>>
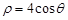 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为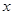 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线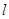 的参数方程是:
的参数方程是: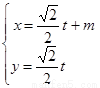 (
(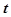 是参数).
是参数).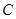 的极坐标方程和直线
的极坐标方程和直线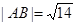 ,试求实数
,试求实数 值.
值. 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
 ;
; .
.