摘要：17． 甲.乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中 随机抽取8次.记录如下: 甲 82 81 79 78 95 88 93 84 乙 92 95 80 75 83 80 90 85 (Ⅰ)用茎叶图表示这两组数据, (Ⅱ)现要从中选派一人参加数学竞赛.从统计学的角度考虑.你认为选派哪位学生参 加合适?请说明理由, (Ⅲ)若将频率视为概率.对甲同学在今后的3次数学竞赛成绩进行预测.记这3次成 绩中高于80分的次数为.求的分布列及数学期望.
网址：http://m.1010jiajiao.com/timu3_id_529143[举报]
（本小题满分13分）
从甲、乙两个班中各随机的抽取6名学生，他们的数学成绩如下：
|
甲班 |
76 |
74 |
82 |
96 |
66 |
76 |
|
乙班 |
86 |
84 |
62 |
76 |
78 |
92 |
(I)画出茎叶图并求出甲班学生的数学成绩的中位数；
(II)若不低于80分则表示该生数学成绩为优秀。现从甲、乙两班中各抽出1名学生参加数学兴趣小组，求这两名学生的数学成绩恰好都优秀的概率。
查看习题详情和答案>>
（本小题满分13分）
为加强大学生实践、创新能力和团队精神的培养，促进高等教育教学改革，教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序.通过预赛，选拔出甲、乙等五支队伍参加决赛.
（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；
（Ⅱ）若决赛中甲队和乙队之间间隔的队伍数记为
，求的分布列和数学期望.
查看习题详情和答案>>
（本小题满分13分）
为加强大学生实践、创新能力和团队精神的培养，促进高等教育教学改革，教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序.通过预赛，选拔出甲、乙等五支队伍参加决赛.
（Ⅰ）求决赛中甲、乙两支队伍恰好排在前两位的概率；
（Ⅱ）若决赛中甲队和乙队之间间隔的队伍数记为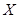
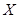，求的分布列和数学期望.
查看习题详情和答案>>
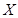，求