摘要:21. 解: (Ⅰ)由题意..得∴ ----1分 当时. . ∴ ------3分 ∴数列是首项.公比为的等比数列.∴ ---4分 知当时. -------5分 ∵.∴ -------------------6分 即 ----------------------------7分 (Ⅲ)∵ = = ------------9分 ∵ ------------------10分 ∴= -12分 由得 -------() ∵()对都成立 ∴ ∵是正整数.∴的值为1,2,3. ∴使对都成立的正整数存在.其值为:1.2.3. --14分 本资料由 提供!
网址:http://m.1010jiajiao.com/timu3_id_528961[举报]
(本小题满分14分)已知函数 满足
满足 ,且
,且 有唯一实数解。
有唯一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记 ,且
,且 =
= ,求数列
,求数列 的通项公式。
的通项公式。
(3)记  ,数列{
,数列{ }的前
}的前  项和为
项和为  ,是否存在k∈N*,使得
,是否存在k∈N*,使得 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
(本小题满分14分)已知函数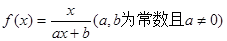 满足
满足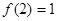 ,且
,且 有唯一实数解。
有唯一实数解。
(1)求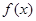 的表达式 ;
的表达式 ;
(2)记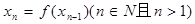 ,且
,且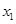 =
=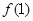 ,求数列
,求数列 的通项公式。
的通项公式。
(3)记 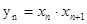 ,数列{
,数列{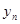 }的前
}的前 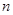 项和为
项和为
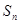 ,是否存在k∈N*,使得
,是否存在k∈N*,使得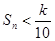 对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
查看习题详情和答案>>
(本小题满分14分)
已知:函数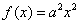 (
(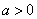 ),
),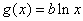 .
.
(1)若函数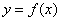 图象上的点到直线
图象上的点到直线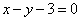 距离的最小值为
距离的最小值为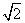 ,求
,求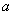 的值;
的值;
(2)关于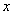 的不等式
的不等式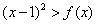 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数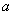 的取值范围;
的取值范围;
(3)对于函数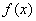 与
与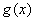 定义域上的任意实数
定义域上的任意实数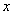 ,若存在常数
,若存在常数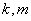 ,使得不等式
,使得不等式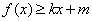 和
和 都成立,则称直线
都成立,则称直线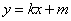 为函数
为函数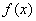 与
与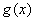 的“分界线”。设
的“分界线”。设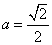 ,
,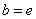 ,试探究
,试探究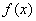 与
与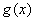 是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程;若不存在,请说明理由.
查看习题详情和答案>>