摘要：如图(21)图.M和N(2.0)是平面上的两点.动点P满足: (Ⅰ)求点P的轨迹方程, (Ⅱ)若,求点P的坐标. 分析:根据已知条件和椭圆的定义易得点P的轨迹方程. 由(2)中的等式可变形转为向量的模和数量积.结合总条件. 在三角形中研究边与角之间的关系.
网址：http://m.1010jiajiao.com/timu3_id_528778[举报]
如右图，M（-2，0）和N（2，0）是平面上的两点，动点P满足：
w.w.w.k.s.5.u.c.o.m 
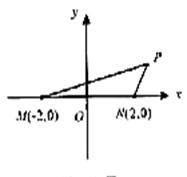
（1）.求点P的轨迹方程；
（2）.若点P到点M距离是到点N距离的2倍，求点P横坐标.
查看习题详情和答案>>如下图，M(－2，0)和N(2，0)是平面上的两点，动点P满足：||PM|－|PN||＝2．
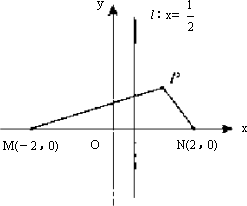
(Ⅰ)求点P的轨迹方程；
(Ⅱ)设d为点P到直线l：
的距离，若|PM|＝2|PN|2，求
的值．
如图，M（-2，0）和N（2，0）是平面上的两点，动点P满足：|PM|+|PN|=6．
如图，M（-2，0）和N（2，0）是平面上的两点，动点P满足：||PM|-|PN||=2．
，求点P的坐标。 