摘要:14. 已知数列中...且. (Ⅰ)设.证明是等比数列, (Ⅱ)求数列的通项公式, (Ⅲ)若是与的等差中项.求的值.并证明:对任意的.是与的等差中项. (Ⅰ)证明:由题设.得 . 即 . 又..所以是首项为1.公比为的等比数列. . . . -- . 将以上各式相加.得.所以当时. 上式对显然成立. .当时.显然不是与的等差中项.故. 由可得.由得 . ① 整理得.解得或.于是 . 另一方面. . . 由①可得 . 所以对任意的.是与的等差中项.
网址:http://m.1010jiajiao.com/timu3_id_528023[举报]
 中,
中,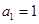 ,
, ,且
,且
 .
.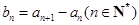 ,求
,求 是的通项公式;
是的通项公式;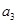 是
是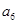 与
与 的等差中项,求
的等差中项,求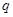 的值,并证明:对任意的
的值,并证明:对任意的 ,
, 是
是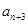 与
与 的等差中项.
的等差中项.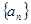 的项构成的新数列
的项构成的新数列 是公比为
是公比为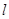 的等比数列,则相应的数列
的等比数列,则相应的数列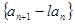 是公比为
是公比为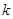 的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列
的等比数列,运用此性质,可以较为简洁的求出一类递推数列的通项公式,并简称此法为双等比数列法.已知数列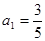 ,
, ,且
,且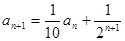 .
.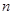 项和
项和
 数列
数列 中,
中, ,
,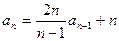
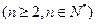 .且
.且 k为等比数列。
k为等比数列。  及数列
及数列 、
、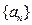 的通项公式;
的通项公式;
 为
为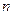 项和,求
项和,求 中,
中, ,
, ,且
,且
 .
. ,求
,求 是的通项公式;
是的通项公式; 是
是 与
与 的等差中项,求
的等差中项,求 的值,并证明:对任意的
的值,并证明:对任意的 ,
, 是
是 与
与 的等差中项.
的等差中项.