摘要:3. 如图.在四棱锥P-ABCD中.侧面PAD⊥底面ABCD.侧棱PA=PD=,底面ABCD为直角梯形.其中BC∥AD,AB⊥AD,AD=2AB=2BC=2.O为AD中点. (Ⅰ)求证:PO⊥平面ABCD, (Ⅱ)求异面直线PB与CD所成角的余弦值, (Ⅲ)求点A到平面PCD的距离. 解法一: (Ⅰ)证明:在△PAD卡中PA=PD.O为AD中点.所以PO⊥AD. 又侧面PAD⊥底面ABCD.平面PAD∩平面ABCD=AD.PO平面PAD. 所以PO⊥平面ABCD. (Ⅱ)连结BO.在直角梯形ABCD中.BC∥AD,AD=2AB=2BC. 有OD∥BC且OD=BC.所以四边形OBCD是平行四边形. 所以OB∥DC. 由(Ⅰ)知PO⊥OB.∠PBO为锐角. 所以∠PBO是异面直线PB与CD所成的角. 因为AD=2AB=2BC=2.在Rt△AOB中.AB=1.AO=1.所以OB=. 在Rt△POA中.因为AP=.AO=1.所以OP=1. 在Rt△PBO中.PB=, cos∠PBO=, 所以异面直线PB与CD所成的角的余弦值为. 得CD=OB=. 在Rt△POC中.PC=. 所以PC=CD=DP.S△PCD=·2=. 又S△= 设点A到平面PCD的距离h. 由VP-ACD=VA-PCD. 得S△ACD·OP=S△PCD·h. 即×1×1=××h. 解得h=. 解法二: (Ⅰ)同解法一. (Ⅱ)以O为坐标原点.的方向分别为x轴.y轴.z轴的正方向.建立空间直角坐标系O-xyz. 则A.B.C. D.P. 所以=.=(t.-1.-1). ∞〈.〉=. 所以异面直线PB与CD所成的角的余弦值为. (Ⅲ)设平面PCD的法向量为n=(x0,y0,x0). 由(Ⅱ)知=.=. 则 n·=0.所以 -x0+ x0=0, n·=0. -x0+ y0=0. 即x0=y0=x0, 取x0=1.得平面的一个法向量为n=. 又=. 从而点A到平面PCD的距离d=
网址:http://m.1010jiajiao.com/timu3_id_527942[举报]
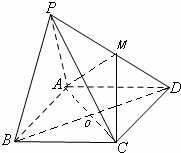 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2| 2 |
(Ⅰ)证明PB∥平面MAC
(Ⅱ)证明平面PAB⊥平面ABCD
(Ⅲ)求四棱锥p-ABCD的体积. 查看习题详情和答案>>
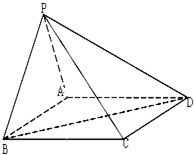 如图,在四棱锥P-ABCD中,底面ABCD是矩形,知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,知AB=3,AD=2,PA=2,PD=2| 2 |
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的余弦值;
(3)求二面角P-BD-A的大小余弦值.
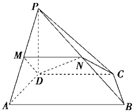 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AD⊥AB,CD∥AB,AB=
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AD⊥AB,CD∥AB,AB=| 2 |
(1)求证:MN∥平面PCD;
(2)求证:四边形MNCD是直角梯形;
(3)求证:DN⊥平面PCB.
 16、如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
16、如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.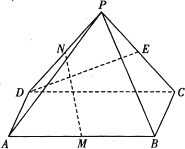 (2011•武汉模拟)如图,在四棱锥P-ABCD中,△PCD为等边三角形,四边形ABCD为矩形,平面PDC丄平面ABCD,M、N、E分别是AB、PD、PC的中点,AB=2AD.
(2011•武汉模拟)如图,在四棱锥P-ABCD中,△PCD为等边三角形,四边形ABCD为矩形,平面PDC丄平面ABCD,M、N、E分别是AB、PD、PC的中点,AB=2AD.