摘要:2. 已知函数. 数列满足 (I)求数列的通项公式, (II)设x轴.直线与函数的图象所围成的封闭图形的面积为.求, (III)在集合.且中.是否存在正整数N.使得不等式对一切恒成立?若存在.则这样的正整数N共有多少个?并求出满足条件的最小的正整数N,若不存在.请说明理由. (IV)请构造一个与有关的数列.使得存在.并求出这个极限值. 解:(I) --1分 -- 将这n个式子相加.得 --3分 (II)为一直角梯形(时为直角三角形)的面积.该梯形的两底边的长分别为.高为1 --6分 (III)设满足条件的正整数N存在.则 又 均满足条件 它们构成首项为2010.公差为2的等差数列. 设共有m个满足条件的正整数N.则.解得 中满足条件的正整数N存在.共有495个. --9分 (IV)设.即 则 显然.其极限存在.并且 --10分 注:.等都能使存在.
网址:http://m.1010jiajiao.com/timu3_id_527769[举报]
 在
在 处取得最值.
处取得最值.  的最小正周期及
的最小正周期及 的值;
的值; 是首项与公差均为
是首项与公差均为 的等差数列,求
的等差数列,求 的值.
的值.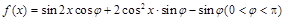 在
在 处取得最值.
处取得最值. 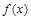 的最小正周期及
的最小正周期及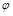 的值;
的值;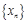 是首项与公差均为
是首项与公差均为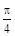 的等差数列,求
的等差数列,求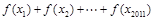 的值.
的值. 满分13分)
满分13分)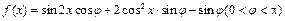 在
在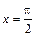 处取得最值.
处取得最值. 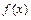 的最小正周期及
的最小正周期及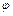 的值;
的值;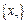 是首项与公差均为
是首项与公差均为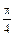 的等差数列,求
的等差数列,求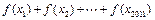 的值.
的值.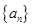 的相邻两项
的相邻两项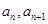 是关于
是关于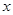 的方程
的方程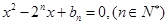 的两根,且
的两根,且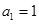
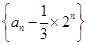 是等比数列;
是等比数列;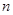 项和
项和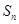 ;
;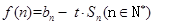 若
若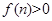 对任意的
对任意的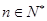 都成立,求
都成立,求 的取值范围。
的取值范围。