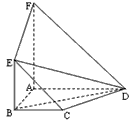
摘要:如图.面ABEF⊥面ABCD.四边形ABEF与四边形ABCD都是直角梯形.∠BAD=∠FAB=90°.BC∥AD.BE∥AF.G.H分别是FA.FD的中点. (Ⅰ)证明:四边形BCHG是平行四边形, (Ⅱ)C.D.E.F四点是否共面?为什么? (Ⅲ)设AB=BE.证明:平面ADE⊥平面CDE.
网址:http://m.1010jiajiao.com/timu3_id_527621[举报]
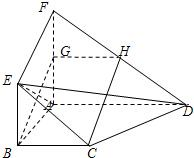 如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么? 查看习题详情和答案>>
如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
AD,BE
AF,G、H分别是FA、FD的中点.
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?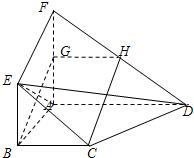
查看习题详情和答案>>
| ||
| . |
| 1 |
| 2 |
| ||
| . |
| 1 |
| 2 |
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?

如图,面ABEF⊥面ABCD,四边形ABEF与四边形ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
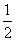 AD,BE
AD,BE
 AF,G、H分别是FA、FD的中点,
AF,G、H分别是FA、FD的中点,
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?
(Ⅲ)设AB=BE,证明:平面ADE⊥平面CDE。

 AD,BE
AD,BE
 AF,G、H分别是FA、FD的中点,
AF,G、H分别是FA、FD的中点,(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C、D、E、F四点是否共面?为什么?
(Ⅲ)设AB=BE,证明:平面ADE⊥平面CDE。
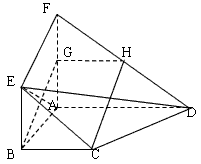
 AD,BE
AD,BE
 AF,G、H分别是FA、FD的中点.
AF,G、H分别是FA、FD的中点.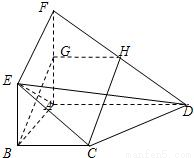

 AD,BE
AD,BE
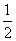 AF.
AF.