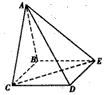
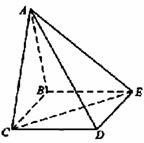
摘要：四棱锥A-BCDE中.底面BCDE为矩形.侧面ABC⊥底面BCDE. BC＝2.CD＝.AB=AC. (1) 证明:AD⊥CE; (2) 设侧面ABC为等边三角形.求二面角C-AD-E的大小.
网址：http://m.1010jiajiao.com/timu3_id_527619[举报]
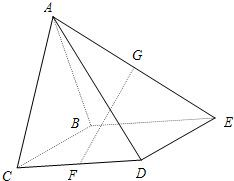四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD=| 2 |
（I）取CD的中点为F，AE的中点为G，证明：FG∥面ABC；
（II）证明：AD⊥CE． 查看习题详情和答案>>
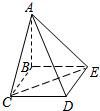四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD=| 2 |
（Ⅰ）证明：AD⊥CE；
（Ⅱ）设CE与平面ABE所成的角为45°，求二面角C-AD-E的大小． 查看习题详情和答案>>
四棱锥A-BCDE中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD=
，AB=AC。
，AB=AC。
（1）证明：AD⊥CE；
（2）设CE与平面ABE所成的角为45°，求二面角C-AD-E的大小。
查看习题详情和答案>>
（2）设CE与平面ABE所成的角为45°，求二面角C-AD-E的大小。
，AB=AC．
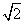，AB=AC.