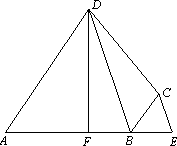摘要:6. ⑴ 连结BD ∵底面ABCD是菱形.∠BCD=90° ∴△BCD是正三角形 ∵点E是BC边的中点 ∴DE⊥BC ∵AD∥BC ∴AD⊥DE ∵PD⊥AD PD∩DE=D ∴AD⊥平面PDE. ⑵ ①∵DE⊥AD.PD⊥AD.∴∠PDE为二面角P-AD-C的平面角 ∵二面角P-AD-C大小等于60° ∴∠PDE=60° 过点P在平面PDE内作PK⊥DE于K.由⑴易证AD⊥PK. ∴PK⊥平面ABCD ∵PD= ∴DK=.PK=4 即点P到平面ABCD的距离为4 ②∵AB=4 ∴DE=2 ∴DK=DE ∴K为△ABD重心 连结BK ∴△BCD是正三角形 ∴BK⊥CD ∵AB∥CD ∴BK⊥AB ∵ PK⊥平面ABCD ∴BK为BP在平面ABCD内的射影. ∴PB⊥AB ∴∠PBK为二面角P-AB-C的平面角 在直角△PKB中.tanPBK= ∴∠PBK= ∴二面角P-AB-C为 解法二: (1)同解法一 (2)①同解法一 ②∵AB=4 ∴DE=2 ∵DK= ∴K为△BCD重心 以点K为坐标原点.建系如图. ∴A(4,- ∴ 设平面PAB的法向量为s=,则 ∴ ∴s=(1, ∴cos<s,>= ∴二面角P-AB-C的大小为
网址:http://m.1010jiajiao.com/timu3_id_527381[举报]
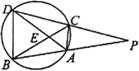
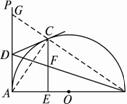
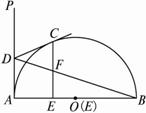
如图13,已知AB为半圆O的直径,AP为过点A的半圆的切线,在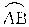 上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E,连结BD,交CE于点F.
上任取一点C(点C与A、B不重合),过点C作半圆的切线CD交AP于点D;过点C作CE⊥AB,垂足为E,连结BD,交CE于点F.
(1) (2)
图13
(1)当点C为![]() 的中点时(如图13(1)),求证:CF =EF;
的中点时(如图13(1)),求证:CF =EF;
(2)当点C不是![]() 的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
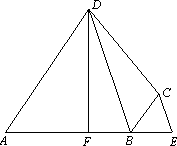
如下图,四边形ABCD中,DF⊥AB,垂足为F,DF=3,AF=2FB=2,延长FB到E,使BE=FB,连结BD,EC若BD∥EC,则四边形ABCD的面积为
[ ]
A.
4
B.
5
C.
6
D.
7