摘要：18．设正项数列{an}的前n项和为Sn.且存在正数t.使得对所有正整数n.t与an的等差中项和t与Sn的等比中项相等.求证数列{}为等差数列.并求{an}通项公式及前n项和．
网址：http://m.1010jiajiao.com/timu3_id_526998[举报]
设正项数列{an}的前n项和为Sn，且a1=2，an+1=2Sn+2（n∈N*），
（1）求a2以及数列{an}的通项公式；
（2）在an与an+1之间插入n个数，使这n个数组成一个公差为dn的等差数列．
（ⅰ）求证：
+
+
+…+
＜
（n∈N*）；
（ⅱ）求证：在数列{dn}中不存在三项dm，ds，dt成等比数列．（其中m，s，t依次成等比数列）
查看习题详情和答案>>
（1）求a2以及数列{an}的通项公式；
（2）在an与an+1之间插入n个数，使这n个数组成一个公差为dn的等差数列．
（ⅰ）求证：
| 1 |
| d1 |
| 1 |
| d2 |
| 1 |
| d3 |
| 1 |
| dn |
| 15 |
| 16 |
（ⅱ）求证：在数列{dn}中不存在三项dm，ds，dt成等比数列．（其中m，s，t依次成等比数列）
设正项数列{an}的前n项和为Sn，且Sn=
an2+
an-
，n∈N*．
（1）求数列{an}的通项公式；
（2）是否存在等比数列{bn}，使a1b1+a2b2+…anbn=（2n-1）•2n+1+2对一切正整数都成立？并证明你的结论．
查看习题详情和答案>>
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
（1）求数列{an}的通项公式；
（2）是否存在等比数列{bn}，使a1b1+a2b2+…anbn=（2n-1）•2n+1+2对一切正整数都成立？并证明你的结论．
an2+
an-
，n∈N*．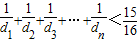
（n∈N*）；
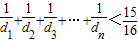（n∈N*）；