摘要:6. 函数的定义域是.且对于任意正数.函数 都是其定义域上的增函数.则函数的图象可能是( ) A B C D
网址:http://m.1010jiajiao.com/timu3_id_526751[举报]
设函数 的定义域为D,若存在非零实数h使得对于任意
的定义域为D,若存在非零实数h使得对于任意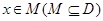 ,有
,有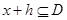 ,且
,且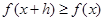 ,则称
,则称 为M上的“h阶高调函数”。给出如下结论:
为M上的“h阶高调函数”。给出如下结论:
①若函数 在R上单调递增,则存在非零实数h使
在R上单调递增,则存在非零实数h使 为R上的“h阶高调函数”;
为R上的“h阶高调函数”;
②若函数 为R上的“h阶高调函数”,则
为R上的“h阶高调函数”,则 在R上单调递增;
在R上单调递增;
③若函数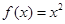 为区间
为区间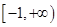 上的“h阶高诬蔑财函数”,则
上的“h阶高诬蔑财函数”,则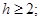
④若函数 在R上的奇函数,且
在R上的奇函数,且 时,
时,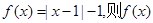 只能是R上的“4阶高调函数”。
只能是R上的“4阶高调函数”。
其中正确结论的序号为 ( )
A.①③ B.①④ C.②③ D.②④
查看习题详情和答案>>
设f(x)的定义域(0,+∞)对于任意正实数m,n恒有f(m·n)=f(m)+f(n),且当![]()
(1)求f(2)的值;
(2)求证:f(x)在(0,+∞)上是增函数;
(3)解关于x的不等式f(x)≥2+f(![]() ),其中p>-1.
),其中p>-1.
定义域是一切实数的函数y=f(x),其图象是连续不断的,且存在常数λ(λ∈R)使得 f(x+λ)+λf(x)=0对任意实数x都成立,则称f(x)是一个“λ一和谐函数”. 有下列关于“λ-和谐函数”的结论:
①f(x)=0是常数函数中唯一一个“λ-和谐函数”;
②f(x)=x不是一个“λ-和谐函数”;
③f(x)=x2是一个“λ-和谐函数”;
④“
-和谐函数”至少有一个零点.
则正确结论的序号为 (写出所有正确结论的序号).
查看习题详情和答案>>
①f(x)=0是常数函数中唯一一个“λ-和谐函数”;
②f(x)=x不是一个“λ-和谐函数”;
③f(x)=x2是一个“λ-和谐函数”;
④“
| 1 | 2 |
则正确结论的序号为