摘要：三位同学在研究函数 f (x) = (x∈R) 时.分别给出下面三个结论: ① 函数 f (x) 的值域为 ② 若x1≠x2.则一定有f (x1)≠f (x2) ③ 若规定 f1(x) = f (x).fn+1(x) = f [ fn(x)].则 fn(x) = 对任意 n∈N* 恒成立. 你认为上述三个结论中正确的个数有 0个 (B) 1个 (C) 2个 (D) 3个
网址：http://m.1010jiajiao.com/timu3_id_526021[举报]
三位同学在研究函数 f (x) = 
(x∈R) 时，分别给出下面三个结论：
① 函数 f (x) 的值域为 (－1,1)
② 若x1≠x2，则一定有f (x1)≠f (x2)
③ 若规定 f1(x) = f (x)，fn+1(x) = f [ fn(x)]，则 fn(x) = 
对任意 n∈N* 恒成立.
你认为上述三个结论中正确的个数有
A．0个 B．1个 C．2个 D．3个
查看习题详情和答案>>三位同学在研究函数f(x)=
（x∈R） 时，分别给出下面三个结论：
①函数f（x）的值域为 （-1，1）
②若x1≠x2，则一定有f（x1）≠f（x2）
③若规定f1（x）=f（x），fn+1（x）=f[fn（x）]，则fn(x)=
对任意n∈N*恒成立．
你认为上述三个结论中正确的个数有______．
查看习题详情和答案>>
| x |
| 1+|x| |
①函数f（x）的值域为 （-1，1）
②若x1≠x2，则一定有f（x1）≠f（x2）
③若规定f1（x）=f（x），fn+1（x）=f[fn（x）]，则fn(x)=
| x |
| 1+n|x| |
你认为上述三个结论中正确的个数有______．
三位同学在研究函数f(x)＝
(x∈R)时，分别给出下面三个结论：
①函数f(x)的值域为(－1，1)
②若x1≠x2，则一定有f(x1)≠f(x2)
③若规定f1(x)＝f(x)，fn+1(x)＝f[fn(x)]，则fn(x)＝
对任意n∈N*恒成立．
你认为上述三个结论中正确的个数有
[ ]
A．0个
B．1个
C．2个
D．3个
（x∈R） 时，分别给出下面三个结论：
对任意n∈N*恒成立．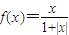
（x∈R） 时，分别给出下面三个结论：
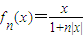对任意n∈N*恒成立．