摘要:已知数列{an}的前n项为和Sn.点在直线上. 数列{bn}满足.前9项和为153. (Ⅰ)求数列{an}.{bn}的通项公式, (Ⅱ)设.数列{cn}的前n和为Tn.求使不等式对一切都成立的最大正整数k的值. (Ⅲ)设.问是否存在.使得成立?若存在.求出m的值,若不存在.请说明理由. 广州市第41中学2008届高三第二次模拟 理科答卷 班级 姓名 学号 成绩
网址:http://m.1010jiajiao.com/timu3_id_525564[举报]
已知数列{an}的前n项为和Sn,点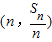 在直线
在直线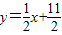 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设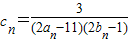 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式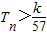 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
(Ⅲ)设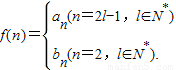 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
查看习题详情和答案>>
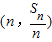 在直线
在直线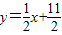 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设
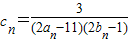 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式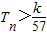 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.(Ⅲ)设
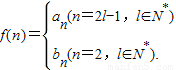 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.查看习题详情和答案>>
已知数列{an}的前n项为和Sn,点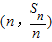 在直线
在直线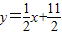 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设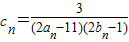 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式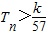 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
(Ⅲ)设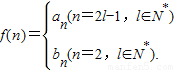 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
查看习题详情和答案>>
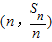 在直线
在直线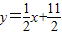 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设
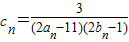 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式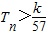 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.(Ⅲ)设
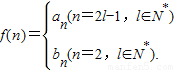 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.查看习题详情和答案>>
已知数列{an}的前n项为和Sn,点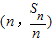 在直线
在直线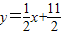 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设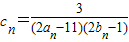 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式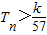 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.
(Ⅲ)设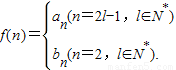 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
查看习题详情和答案>>
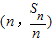 在直线
在直线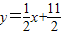 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)设
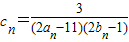 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式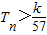 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值.(Ⅲ)设
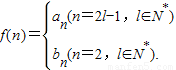 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.查看习题详情和答案>>
 在直线
在直线 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153. ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值. 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.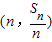 在直线
在直线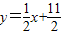 上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.
上.数列{bn}满足bn+2-2bn+1+bn=0(n∈N*),且b3=11,前9项和为153.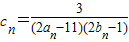 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式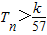 对一切n∈N*都成立的最大正整数k的值.
对一切n∈N*都成立的最大正整数k的值. 是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
是否存在m∈N*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.