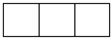
摘要: 某工厂拟建一座平面图为矩形且面积为200m2 的三级污水处理池.如果池外周壁建造单价为每米400元.中间两条隔墙建造单价为每米248元.池底建造单价为每平方米80元(池壁厚度忽略不计.且池无盖). 与污水处理池长x , (2)若由于地形限制.长.宽都不能超过16m.求f(x)的定义域; 下.污水处理池的长和宽各为多少时.污水处理池的总造价最低?并求出最低总造价. 解析:①因污水处理水池的长为 . 由题设条件即函数定义域为[12.5,16] ②先研究函数上的单调性. 对于任意的 则 又 故函数y=f(x)在[12.5,16]上是减函数. ∴当x=16时.y取得最小值.此时 综上.当污水处理池的长为16m.宽为12.5m时.总造价最低.最低为45000元.
网址:http://m.1010jiajiao.com/timu3_id_524210[举报]
 某工厂拟建一座平面图(如图所示)为矩形且面积为200m2的三级污水处理池,由于地形限制,长、宽都不能超过16m.如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).
某工厂拟建一座平面图(如图所示)为矩形且面积为200m2的三级污水处理池,由于地形限制,长、宽都不能超过16m.如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).(1)写出总造价y(元)与污水处理池长x(m)的函数关系式,并指出其定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求出最低总造价. 查看习题详情和答案>>
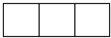
 某工厂拟建一座平面图为矩形且面积为400平方米的三级污水处理池,平面图如图所示,池外圈建造单价为每米200元,中间两条隔墙建造单价为每米250元,池底建造单价为每平方米80元(池壁的厚度忽略不计且池无盖).若受场地限制,长与宽都不能超过25米,则污水池的最低造价为多少?
某工厂拟建一座平面图为矩形且面积为400平方米的三级污水处理池,平面图如图所示,池外圈建造单价为每米200元,中间两条隔墙建造单价为每米250元,池底建造单价为每平方米80元(池壁的厚度忽略不计且池无盖).若受场地限制,长与宽都不能超过25米,则污水池的最低造价为多少? 某工厂拟建一座平面图为矩形且面积为400平方米的三级污水处理池,平面图如图所示,池外圈建造单价为每米200元,中间两条隔墙建造单价为每米250元,池底建造单价为每平方米80元(池壁的厚度忽略不计且池无盖).若受场地限制,长与宽都不能超过25米,则污水池的最低造价为多少?
某工厂拟建一座平面图为矩形且面积为400平方米的三级污水处理池,平面图如图所示,池外圈建造单价为每米200元,中间两条隔墙建造单价为每米250元,池底建造单价为每平方米80元(池壁的厚度忽略不计且池无盖).若受场地限制,长与宽都不能超过25米,则污水池的最低造价为多少?