摘要：设A=.B=,若AB.求实数a的取值范围. 解:由图象法解得: 当a>0时., 当a≤0时. ∴要使得AB.必须且只须.解得
网址：http://m.1010jiajiao.com/timu3_id_523621[举报]
设A，B分别是直线y=
x和y=-
x上的两个动点，并且|
|=
，动点P满足
=
+
．记动点P的轨迹为C．
（I） 求轨迹C的方程；
（Ⅱ）若点D的坐标为（0，16），M、N是曲线C上的两个动点，且
=λ
，求实数λ的取值范围．
查看习题详情和答案>>
2
| ||
| 5 |
2
| ||
| 5 |
| AB |
| 20 |
| OP |
| OA |
| OB |
（I） 求轨迹C的方程；
（Ⅱ）若点D的坐标为（0，16），M、N是曲线C上的两个动点，且
| DM |
| DN |
设a∈R，向量m=（a，1），函数y=f（x）的图象经过坐标原点，f′（x）是函数f（x）的导函数．已知A（-1，f′（-1）），B（x，x2），f′（x）=
•m．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若方程f(x)=
(x+1)2-
在区间[-1，1]上有两个不相等的实数根，求a的取值范围；
（Ⅲ）若a=2，设数列{an}满足a1=3，4an=2f'（an-1）-3（n=2，3，4，…）．求证：an＞22n-1-1（n∈N*）． 查看习题详情和答案>>
| AB |
（Ⅰ）求f（x）的解析式；
（Ⅱ）若方程f(x)=
| a |
| 2 |
| x2 |
| 4 |
（Ⅲ）若a=2，设数列{an}满足a1=3，4an=2f'（an-1）-3（n=2，3，4，…）．求证：an＞22n-1-1（n∈N*）． 查看习题详情和答案>>
设a=
,b=(4sinx,cosx-sinx),f(x)=a·b.
（1）求函数f(x)的解析式；
（2）已知常数
＞0，若y=f(x)在区间
上是增函数，求的取值范围；
（3）设集合A=
，B={x||f(x)-m|＜2},若A
B，求实数m的取值范围.
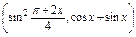,b=(4sinx,cosx-sinx),f(x)=a·b.
＞0，若y=f(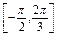
上是增函数，求
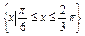，B={x||f(x)-m|＜2},若A
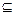B，求实数m的取值范围.
}，B={
}，（1）若A
B={2}，求实数
值；（2）若A
B=A，求实数