摘要:如图.为半圆.AB为半圆直径.O为半圆圆心.且OD⊥AB.Q为线段OD的中点.已知|AB|=4.曲线C过Q点.动点P在曲线C上运动且保持|PA|+|PB|的值不变. (1)建立适当的平面直角坐标系.求曲线C的方程, (2)过D点的直线l与曲线C相交于不同的两点M.N.且M在D.N之间.设=λ.求λ的取值范围. [学法指导]怎样学好圆锥曲线 圆锥曲线将几何与代数进行了完美结合.借助纯代数的解决手段研究曲线的概念和性质及直线与圆锥曲线的位置关系.从数学家笛卡尔开创了坐标系那天就已经开始. 高考中它依然是重点.主客观题必不可少.易.中.难题皆有.为此需要我们做到:
网址:http://m.1010jiajiao.com/timu3_id_522327[举报]
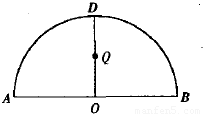
如图,![]() 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设![]() =λ,求λ的取值范围.
=λ,求λ的取值范围.
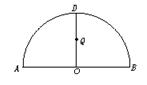
如图,![]() 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设![]() =λ,求λ的取值范围.
=λ,求λ的取值范围.

如图, 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设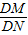 =λ,求λ的取值范围.
=λ,求λ的取值范围.
 查看习题详情和答案>>
查看习题详情和答案>>
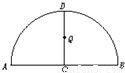
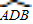 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.(1)建立适当的平面直角坐标系,求曲线C的方程;
(2)过D点的直线l与曲线C相交于不同的两点M、N,且M在D、N之间,设
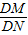 =λ,求λ的取值范围.
=λ,求λ的取值范围. 查看习题详情和答案>>
查看习题详情和答案>>
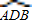 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.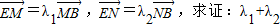 为定值.
为定值.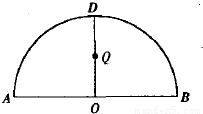
 为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.
为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,已知|AB|=4,曲线C过Q点,动点P在曲线C上运动且保持|PA|+|PB|的值不变.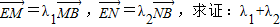 为定值.
为定值.