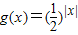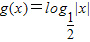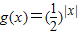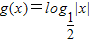摘要：22． 设函数g()对任意的.∈(0.+).都有g(·)=g() + g()成立.又g(2) = 1,已知点pn(an.bn)(n ∈ N* )都在直线: = 2 + 2上.P1为直线与轴的交点.数列{bn}满足n ≥ 2时.bn >0.且g(sn) = g(bn) + g(2+bn) - 2,(n ∈ N* ).其中Sn是数列{bn}的前n项和． (1)求数列{an}.{bn}的通项公式, (2)若(n) = 是否存在∈N*.使得(+5)=2()-2成立? 若存在.求出值,若不存在.说明理由, (3)求证:+ + - + < ．
网址：http://m.1010jiajiao.com/timu3_id_521513[举报]
设函数f（x）=x2+2lnx，用f'（x）表示f（x）的导函数，g(x)=(x2-
)f′(x)，（其中m∈R，且m＞0．）
（1）求函数f（x）的单调区间；
（2）若对任意的x1、x2∈[
，1]都有f'（x1）≤g'（x2）成立，求实数m的取值范围；
（3）试证明：对任意正数a和正整数n，不等式[f'（a）]n-2n-1f'（an）≥2n（2n-2）恒成立．
查看习题详情和答案>>
| m2 |
| 12 |
（1）求函数f（x）的单调区间；
（2）若对任意的x1、x2∈[
| 1 |
| 3 |
（3）试证明：对任意正数a和正整数n，不等式[f'（a）]n-2n-1f'（an）≥2n（2n-2）恒成立．
设函数f(x)、g(x)的定义域分别为F、G，且FG.若对任意的x∈F，都有g(x)＝f(x)，则称g(x)为f(x)在G上的一个“延拓函数”．已知函数f(x)＝(
)x(x≤0)，若g(x)为f(x)在R上的一个延拓函数，且g(x)是偶函数，则函数g(x)的解析式为________．
设函数f（x），g（x）的定义域分别为F、G，且F、G．若对任意的x∈F，都有g（x）=f（x），则称g（x）为f（x）在G上的一个“延拓函数”．已知函数f（x）=2x（x≤0），若g（x）为f（x）在R上一个延拓函数，且g（x）是偶函数，则函数g（x）的解析式是（ ）
A．g（x）=2|x|
B．g（x）=log2|x|
C．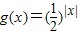
D．
查看习题详情和答案>>
A．g（x）=2|x|
B．g（x）=log2|x|
C．
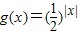
D．
查看习题详情和答案>>
