摘要:22. (1) 当n >1时, bn = Bn –Bn – 1 = –= 3n-2 令n = 1得b1=1, ∴bn=3n-2. 5分 (2)由an= (1+) a n – 1 .得 ∴an= 由a1 = 2 ,bn=3n-2知. an=(1+)(1 + )-(1+)2 =(1+1)(1+)-(1+) 又= = , 5分 设cn= , 当n=1时.有(1+1) = > 当n=2时.有an=(1+1)(1+) = = > = = cn 假设n=k时an>cn成立.即(1+1)(1+)-(1+)>成立, 则n=k+1时. 左边== (1+1)(1+)-(1+)(1+) >(1+)= 3分 右边= c k + 1= = 由(ak+1)3 – (c k + 1)3 =– = =>0, 得ak+1 > c k + 1成立. 综合上述, an>cn对任何正整数n都成立. 3分
网址:http://m.1010jiajiao.com/timu3_id_521353[举报]
下列说法中,正确的是
①任取x∈R都有3x>2x ②当a>1时,任取x∈R都有ax>a-x ③y=(![]() )-x是增函数 ④y=2|x|的最小值为1 ⑤在同一坐标系中,y=2x与y=2-x的图象对称于y轴
)-x是增函数 ④y=2|x|的最小值为1 ⑤在同一坐标系中,y=2x与y=2-x的图象对称于y轴
A.①②④ B.④⑤
C.②③④ D.①⑤
查看习题详情和答案>> 令
令 令当n>1时,
令当n>1时, 则
则 ,
,  .
.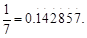 令
令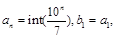 令当n>1时,
令当n>1时,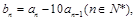 则
则 ,
,  .
.