摘要:已知三次函数在和时取极值.且. (1) 求函数的表达式, (2) 求函数的单调区间和极值, (3) 若函数在区间上的值域为.试求.应满足的条件. 解:(1) . 由题意得.是的两个根. 解得.. 再由可得. ∴. (2) . 当时.,当时., 当时.,当时., 当时.. ∴函数在区间上是增函数, 在区间上是减函数,在区间上是增函数. 函数的极大值是.极小值是. (3) 函数的图象是由的图象向右平移个单位.向上平移4个单位得到的. 所以.函数在区间上的值域为(). 而.∴.即. 于是.函数在区间上的值域为. 令得或. 由的单调性知..即. 综上所述..应满足的条件是:.且. 易错问题
网址:http://m.1010jiajiao.com/timu3_id_520912[举报]
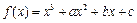 在
在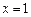 和
和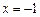 时取极值,且
时取极值,且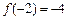 .
.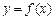 的表达式;
的表达式;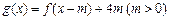 在区间
在区间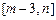 上的值域为
上的值域为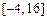 ,试求
,试求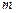 、n应满足的条件。
、n应满足的条件。