摘要：23．设f(n)＝2n+1(n∈N).P＝{1.2.3.4.5}.Q＝{3.4.5.6.7}.记＝{n∈N|f(n)∈P}.＝{n∈N|f(n)∈Q}.则(∩)∪(∩)＝ {1.2} {1.2.6.7}
网址：http://m.1010jiajiao.com/timu3_id_520425[举报]
设定义在(0，＋∞)上的函数f(x)满足：①对于任意的a、b，都有f(a·b)＝f(a)＋f(b)－p，其中：p为正实数；②f(2)＝p－1；③当x＞1时，总有f(x)＜p．
(Ⅰ)求f(1)及
的值；(用含p的式子表示)；
(Ⅱ)求证：f(x)在(0，＋∞)上为减函数；
(Ⅲ)设an＝f(2n)(n∈N*)，数列{an}的前n项的和为Sn，当且仅当n＝5时，Sn取得最大值，求p的取值范围．
)，P＝{1,2,3,4,5}，M＝{3,4,5,6,7}．记
，
，则
设f(n)＝2n＋1(n∈N)，P＝{1，2，3，4，5}，Q＝{3，4，5，6，7}，记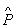
＝{n∈N|f(n)∈P}，
＝{n∈N|f(n)∈Q}，则(
∩CN
)∪(
∩CN
)＝( )
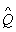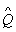＝{n∈N|f(n)∈P}，＝{n∈N|f(n)∈Q}，则(∩CN)∪(∩CN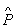)＝( )(A) {0，3} (B){1，2} (C) (3，4，5) (D){1，2，6，7}
查看习题详情和答案>>
＝{n∈N|f(n)∈P}，
＝{n∈N|f(n)∈Q}，则(
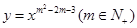的图象与x轴，y轴无交点且关于原点对称，又有函数f(x)=x2－alnx+m－2在(1，2]上是增函数，g(x)=x－
在(0,1)上为减函数.
，数列{an}满足a1＝1，an+1＝p(an)，（n∈N+），数列{bn}，满足
，
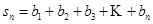，求数列{an}的通项公式an和sn.
，试比较[h(x)]n+2与h(xn)+2n的大小（n∈N+），并说明理由.