摘要:18. 袋中装有大小相等的3个白球.2个红球和个黑球.现从中任取2个球.每取得一个白球得1分.每取得一个红球得2分.每取得一个黑球0分.用表示所得分数.已知得0分的概率为. (Ⅰ)袋中黑球的个数, (Ⅱ)的概率分布列及数学期望.
网址:http://m.1010jiajiao.com/timu3_id_520346[举报]
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重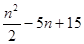 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为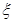 ,求E
,求E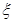 .
.
查看习题详情和答案>>
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为 ,求E
,求E .
.
(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重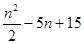 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为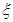 ,求E
,求E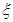 .
.
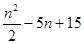 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为
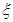 ,求E
,求E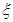 .
.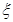 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: