摘要:18.解:(1)∵.∴. --2分 ∵函数在处的切线方程为. ∴.∴--------------------5分 (2)∵点在直线上. ∴.∴. ∵在的图象上.∴. ∴----------------7分 由(1)得:. 令.则.因此函数的单调递增区间为.--9分 令.则.因此函数的单调递减区间为 ∴当时.函数取得极小值---------------12分
网址:http://m.1010jiajiao.com/timu3_id_520046[举报]
设函数
(1)当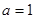 时,求曲线
时,求曲线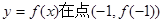 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数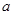 的取值范围.
的取值范围.
【解析】(1)中,先利用 ,表示出点
,表示出点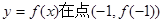 的斜率值
的斜率值 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当 ,再令
,再令 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当 ……2分
……2分
 ∴
∴
即 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令 ………………6分
………………6分
∴ 递减,在(3,+
递减,在(3,+ )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)
①若 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若
∵ 恒成立,
恒成立,
 恒成立,即a>0……………11分
恒成立,即a>0……………11分
 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数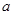 的取值范围是
的取值范围是
查看习题详情和答案>>
已知函数![]()
(1)若函数![]() 时有极值且在函数图象上的点(0,1)处的切线与直线
时有极值且在函数图象上的点(0,1)处的切线与直线![]() 的解析式;
的解析式;
(2)当![]() 取得极大值且加
取得极大值且加![]() 取得极小值时,设点M(
取得极小值时,设点M(![]() )所在平面区域为S,经过原点的直线L将S分别面积比为1:3的两部分求直线L的方程。
)所在平面区域为S,经过原点的直线L将S分别面积比为1:3的两部分求直线L的方程。
已知函数f(x)=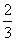 x3+ax2+bx+c.
x3+ax2+bx+c.
(Ⅰ)若函数f(x)在x=1时有极值且在函数图像上的点(0,1)处的切线与直线3x+y=0平行,求f(x)的解析式;
(Ⅱ)当f(x)在x∈(0,1)取得极大值且在x∈(1,2)取得极小值时,设点M(b-2,a+1)所在平面区域为S,经过原点的直线L将S分为面积比为1:3的两部分,求直线L的方程.
查看习题详情和答案>> ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值. ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.