摘要:21.[解] (1)∵F0(c.0)F1(0.).F2(0.) ∴| F0F1 |=.| F1F2 |= 于是..所求“果圆 方程为 (x≥0).(x≤0). --4分 (2)由题意.得a+c>2b.即. ∵(2b)2>b2+c2.∴a2-b2>(2b-a)2.得 --7分 又b2>c2=a2-b2.∴. ∴. (3)设“果圆 的方程为(x≥0)(x≤0) 记平行弦的斜率为k. 当k=0时.直线y=t(-b≤t≤b)与半椭圆(x≥0)的交点是 .与半椭圆(x≤0)的交点是Q(). ∴P.Q的中点M(x.y)满足 得. ∵a<2b.∴. 综上所述.当k=0时.“果圆 平行弦的中点轨迹总是落在某个椭圆--14分 当k>0时.以k为斜率过B1的直线l与半椭圆(x≥0)的交点是 由此.在直线l右测.以k为斜率的平行弦的中点轨迹在直线上.即不在某一椭圆上. --17分 当k<0时.可类似讨论得到平行弦中点轨迹不都在某一椭圆上. --18分 上海文 21.(本题满分18分)本题共有3个小题.第1小题满分4分.第2小题满分5分.第3小题满分9分. 我们把由半椭圆 与半椭圆 合成的曲线称作“果圆 .其中... 如图.设点..是相应椭圆的焦点..和.是“果圆 与.轴的交点.是线段的中点. (1)若是边长为1的等边三角形.求该 “果圆 的方程, (2)设是“果圆 的半椭圆 上任意一点.求证:当取得最小值时. 在点或处, (3)若是“果圆 上任意一点.求取得最小值时点的横坐标.
网址:http://m.1010jiajiao.com/timu3_id_519644[举报]
已知函数f1(x)=3|x-p1|,f2(x)=2•3|x-p2|(p1,p2为实数),函数f(x)定义为:对于每个给定的x,f(x)=
.
(1)讨论函数f1(x)的奇偶性;
(2)解不等式:f2(x)≥6;
(3)若f(x)=f1(x)对任意实数x都成立,求p1,p2满足的条件.
查看习题详情和答案>>
|
(1)讨论函数f1(x)的奇偶性;
(2)解不等式:f2(x)≥6;
(3)若f(x)=f1(x)对任意实数x都成立,求p1,p2满足的条件.
已知函数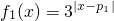 ,
,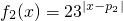 (p1,p2为实数),函数f(x)定义为:对于每个给定的x,
(p1,p2为实数),函数f(x)定义为:对于每个给定的x,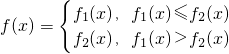 .
.
(1)讨论函数f1(x)的奇偶性;
(2)解不等式:f2(x)≥6;
(3)若f(x)=f1(x)对任意实数x都成立,求p1,p2满足的条件.
查看习题详情和答案>>
已知函数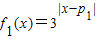 ,
,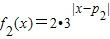 (p1,p2为实数),函数f(x)定义为:对于每个给定的x,
(p1,p2为实数),函数f(x)定义为:对于每个给定的x,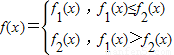 .
.
(1)讨论函数f1(x)的奇偶性;
(2)解不等式:f2(x)≥6;
(3)若f(x)=f1(x)对任意实数x都成立,求p1,p2满足的条件.
查看习题详情和答案>>
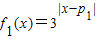 ,
,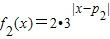 (p1,p2为实数),函数f(x)定义为:对于每个给定的x,
(p1,p2为实数),函数f(x)定义为:对于每个给定的x,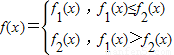 .
.(1)讨论函数f1(x)的奇偶性;
(2)解不等式:f2(x)≥6;
(3)若f(x)=f1(x)对任意实数x都成立,求p1,p2满足的条件.
查看习题详情和答案>>