摘要:18. 设是公比大于1的等比数列.为数列的前项和.已知.且 构成等差数列. (1)求数列的通项, (2)令求数列的前项和.
网址:http://m.1010jiajiao.com/timu3_id_518903[举报]
(本小题满分14分)
当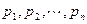 均为正数时,称
均为正数时,称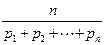 为
为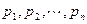 的“均倒数”.已知数列
的“均倒数”.已知数列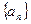 的各项均为正数,且其前
的各项均为正数,且其前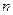 项的“均倒数”为
项的“均倒数”为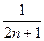 .
.
(1)求数列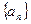 的通项公式;
的通项公式;
(2)设
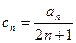
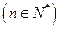 ,试比较
,试比较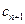 与
与 的大小;
的大小;
(3)设函数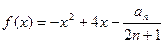 ,是否存在最大的实数
,是否存在最大的实数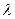 ,使当
,使当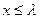
 时,对于一切正
时,对于一切正 整数
整数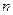 ,都有
,都有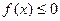 恒成立?
恒成立?
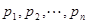 均为正数时,称
均为正数时,称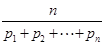 为
为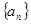 的各项均为正数,且其前
的各项均为正数,且其前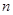 项的“均倒数”为
项的“均倒数”为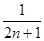 .
.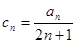
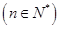 ,试比较
,试比较 与
与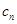 的大小;
的大小;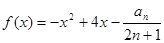 ,是否存在最大的实数
,是否存在最大的实数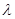 ,使当
,使当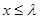 时,对于一切正整数
时,对于一切正整数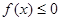 恒成立?
恒成立? 均为正数时,称
均为正数时,称 为
为 的各项均为正数,且其前
的各项均为正数,且其前 项的“均倒数”为
项的“均倒数”为 .
.

 ,试比较
,试比较 与
与 的大小;
的大小; ,是否存在最大的实数
,是否存在最大的实数 ,使当
,使当
 时,对于一切正
时,对于一切正 恒成立?
恒成立?