摘要: 对称 P(.)关于点(.)的对称点为:Q(.) P(.)关于轴的对称点为Q(.) P(.)关于轴的对称点为Q(.) P(.)关于的对称点为Q(.) P(.)关于的对称点为Q(.) P(.)关于的对称点为Q(.) P(.)关于的对称点为Q(.) [典型例题] [例1] 求点A(.4)关于直线:的对称点. 解: 设A关于的对称点B(.) ∴ B(.) [例2] :.:.求关于对称的直线的方程. 解: A(0.1)在点.它关于的对称点.B(.) 由两点式 ∴ : [例3] 光线通过点P(2.3)在直线上反射.反射线过点Q(1.1).求入射光线.反射光线所在直线方程. 解: (2.3)点关于直线的对称点.(.) 由两点式: 交点(.) 由两点式: [例4] 正中A.求三边所在直线方程. 解: ∴ AM交于BC于D.M分之比 ∴ D=(7.4) ∴ : 设AB.AC为: ∴ [例5] ABC中.A.内心I(4.1).求C 解: AI∥轴 ∴ ∴ : 利用三角公式 ∴ ∴ : ∴ C(.4) [例6] 已知中.A(.2)B.求C 解: ∴ 不存在 ∴ ∴ ∴ : C(6.) [例7] 已知.A(6.3).B(.).C(.)求. 解: 作图.为BC到HC的角 ∴ ∴ ∴ [例8] 中.AB.BC.CA边的中点为D(.)E.求三边所在直线方程. 解: ∴ :即 同理: : [例9] .A(.).B(6.).C(.).求的角平分线AT所在直线方程. 解: 设斜率为 CA到AT的角等于AT到AB的角 或 ∴ : [例10] 中.A(.)两条中线所在直线方程为..求BC边所在直线方程. 解: G(.2) G分之比 ∴ D(.5) 设B(.) ∴ C(.) ∴ 两点式: [模拟试题]
网址:http://m.1010jiajiao.com/timu3_id_517951[举报]
已知圆![]() ,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量
,坐标原点为O.圆C上任意一点A在x轴上的射影为点B,已知向量![]() .
.
(1)求动点Q的轨迹E的方程;
(2)当![]() 时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
时,设动点Q关于x轴的对称点为点P,直线PD交轨迹E于点F(异于P点),证明:直线QF与x轴交于定点,并求定点坐标.
 已知椭圆
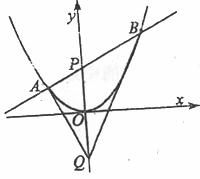
已知椭圆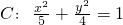 的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且
的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且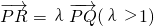 .
. ,求直线l的方程;
,求直线l的方程;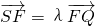 .
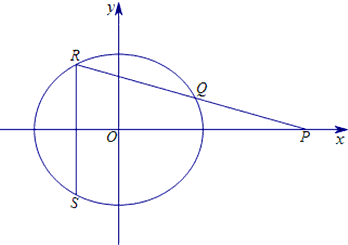
. 如图过抛物线
如图过抛物线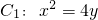 的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是P关于原点的对称点,以P,Q为焦点的椭圆为C2.
的对称轴上一点P(0,m)(m>0)作直线l与抛物线交于A(x1,y1),B(x2,y2)两点,点Q是P关于原点的对称点,以P,Q为焦点的椭圆为C2. ,若
,若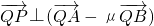 ,求证:λ=μ
,求证:λ=μ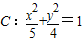 的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且
的右焦点为F,过点P(5,0)的直线l与椭圆C交于Q、R,且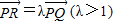 .
.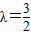 ,求直线l的方程;
,求直线l的方程;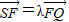 .
.