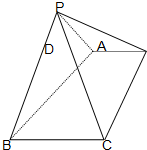如图：已知四棱锥P-ABCD的底面为直角梯形，AD∥BC，∠BCD=90，PA=PB，PC=PD．
（Ⅰ）证明CD与平面PAD不垂直；
（Ⅱ）证明平面PAB⊥平面ABCD；
（Ⅲ）如果CD=AD+BC，二面角P-BC-A等于60°，求二面角P-CD-A的大小．

如图，正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直，△ABE是等腰直角三角形，AB=AE，FA=FE，∠AEF=45°．
（I）求证：EF⊥平面BCE；
（II）设线段CD的中点为P，在直线AE上是否存在一点M，使得PM∥平面BCE？若存在，请指出点M的位置，并证明你的结论；若不存在，请说明理由；
（III）求二面角F-BD-A的余弦值．

（2013•盐城三模）在平面直角坐标系xOy中，椭圆C：

x2

m

+

y2

8-m

=1．
（1）若椭圆C的焦点在x轴上，求实数m的取值范围；
（2）若m=6，
①P是椭圆C上的动点，M点的坐标为（1，0），求PM的最小值及对应的点P的坐标；
②过椭圆C的右焦点F 作与坐标轴不垂直的直线，交椭圆C于A，B两点，线段AB的垂直平分线l交x轴于点N，证明：

AB

FN

 是定值，并求出这个定值．

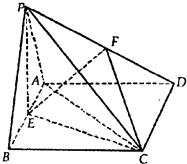（2011•焦作一模）如图：已知△PAB所在的平面与菱形ABCD所在的平面垂直，且PA=PB=

2

2

AB，∠ABC=60°，E为AB的中点．   
（Ⅰ）证明：CE⊥PA；
（Ⅱ）若F为线段PD上的点，且EF与平面PEC的夹角为45°，求平面EFC与平面PBC夹角的余弦值．

已知（如图）在正三棱柱（底面正三角形，侧棱垂直于底面）ABC-A₁B₁C₁中，若AB=AA₁=4，点D是AA₁的中点，点P是BC₁中点
（1）证明DP与平面ABC平行．
（2）是否存在平面ABC上经过C点的直线与DB垂直，如果存在请证明；若不存在，请说明理由．
（3）求四棱锥C₁-A₁B₁BD的体积．