摘要:考试要求:1.掌握平面的基本性质.会用斜二侧的画法画水平放置的平面图形的直观图,能够画出空间两条直线.直线和平面的各种位置关系的图形.能够根据图形想象它们的位置关系.2.掌握直线和平面平行的判定定理和性质定理,理解直线和平面垂直的概念.掌握直线和平面垂直的判定定理,掌握三垂线定理及其逆定理.3.理解空间向量的概念.掌握空间向量的加法.减法和数乘.4.了解空间向量的基本定理,理解空间向量坐标的概念.掌握空间向量的坐标运算.5.掌握空间向量的数量积的定义及其性质,掌握用直角坐标计算空间向量数量积的公式,掌握空间两点间距离公式.6.理解直线的方向向量.平面的法向量.向量在平面内的射影等概念.7.掌握直线和直线.直线和平面.平面和平面所成的角.距离的概念.对于异面直线的距离.只要求会计算已给出公垂线或在坐标表示下的距离.掌握直线和平面垂直的性质定理.掌握两个平面平行.垂直的判定定理和性质定理.8.了解多面体.凸多面体的概念.了解正多面体的概念.9.了解棱柱的概念.掌握棱柱的性质.会画直棱柱的直观图.10.了解棱锥的概念.掌握正棱锥的性质.会画正棱锥的直观图.11.了解球的概念.掌握球的性质.掌握球的表面积.体积公式.
网址:http://m.1010jiajiao.com/timu3_id_517843[举报]
(本题满分14分)
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
105 |
已知在全部105人中抽到随机抽取1人为优秀的概率为
(1)请完成上面的列联表;
(2)根据列联表的数据,若按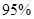 的可靠性要求,能否认为“成绩与班级有关系” .
的可靠性要求,能否认为“成绩与班级有关系” .
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到6或10号的概率.
查看习题详情和答案>>
有甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.
|
|
优秀 |
非优秀 |
总计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
105 |
已知在全部105人中随机抽取一人为优秀的概率为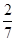 .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到10或11号的概率.
参考公式和数据: 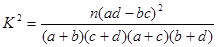
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
查看习题详情和答案>>
甲乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的列联表.

已知在全部105人中随机抽取1人,被抽到的人成绩为优秀的概率为2/7.
(1)请完成上面的列联表;
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”?
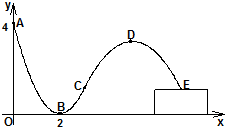 轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.
轮滑是穿着带滚轮的特制鞋在坚硬的场地上滑行的运动.如图,助跑道ABC是一段抛物线,某轮滑运动员通过助跑道获取速度后飞离跑道然后落到离地面高为1米的平台上E处,飞行的轨迹是一段抛物线CDE(抛物线CDE与抛物线ABC在同一平面内),D为这段抛物线的最高点.现在运动员的滑行轨迹所在平面上建立如图所示的直角坐标系,x轴在地面上,助跑道一端点A(0,4),另一端点C(3,1),点B(2,0),单位:米.(Ⅰ)求助跑道所在的抛物线方程;
(Ⅱ)若助跑道所在抛物线与飞行轨迹所在抛物线在点C处有相同的切线,为使运动员安全和空中姿态优美,要求运动员的飞行距离在4米到6米之间(包括4米和6米),试求运动员飞行过程中距离平台最大高度的取值范围?
(注:飞行距离指点C与点E的水平距离,即这两点横坐标差的绝对值.)
 对应的点Z,(1)在复平面的x轴上方;(2)在直线x+y+7=0上.
对应的点Z,(1)在复平面的x轴上方;(2)在直线x+y+7=0上.