摘要：某汽车厂有一条价值为a万元的汽车生产线.现要通过技术改造来提高该生产线的生产能力.提高产品的增加值．经过市场调查.产品的增加值y万元与技术改造投入x万元之间满足:①y与和的乘积成正比,②当时.y=．并且技术改造投入比率:.其中t是常数.且． (1)设y=f(x).求f(x)的表达式及定义域, (2)求出产品增加值y的最大值及相应的x的值．
网址：http://m.1010jiajiao.com/timu3_id_517646[举报]
某汽车厂有一条价值为a万元的汽车生产线，现要通过技术改造来提高该生产线的生产能力，提高产品的增加值，经过市场调查，产品的增加值y万元与技术改造投入x万元之间满足：①y与（a-x）•x2成正比；②当x=
时，y=a3，并且技术改造投入满足
∈（0，t]，其中t为常数且t∈（1，2]．
（1）求y=f（x）表达式及定义域；
（2）求出产品增加值的最大值及相应x的值．
查看习题详情和答案>>
| a |
| 2 |
| x |
| 2(a-x) |
（1）求y=f（x）表达式及定义域；
（2）求出产品增加值的最大值及相应x的值．
某汽车厂有一条价值为a万元的汽车生产线，现要通过技术改造来提高该生产线的生产能力，提高产品的增加值，经过市场调查，产品的增加值y万元与技术改造投入x万元之间满足：①y与（a-x）•x2成正比；②当x=
时，y=a3，并且技术改造投入满足
∈(0，t]，其中t为常数且t∈（1，2]．则函数y=f（x）表达式为
查看习题详情和答案>>
| a |
| 2 |
| x |
| 2(a-x) |
f（x）=8（a-x）x2
f（x）=8（a-x）x2
，定义域(0，
]
| 2at |
| 2t+1 |
(0，
]
．| 2at |
| 2t+1 |
某汽车厂有一条价值为a万元的汽车生产线，现要通过技术改造来提高该生产线的生产能力，提高产品的增加值，经过市场调查，产品的增加值y万元与技术改造投入x万元之间满足：①y与（a-x）•x2成正比；②当x=
时，y=a3，并且技术改造投入满足
∈（0，t]，其中t为常数且t∈（1，2]．
（1）求y=f（x）表达式及定义域；
（2）求出产品增加值的最大值及相应x的值．
查看习题详情和答案>>
时，y=a3，并且技术改造投入满足∈（0，t]，其中t为常数且t∈（1，2]．（1）求y=f（x）表达式及定义域；
（2）求出产品增加值的最大值及相应x的值．
查看习题详情和答案>>
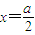时，y=a3，并且技术改造投入满足
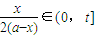，其中t为常数且t∈（1，2]．则函数y=f（x）表达式为 ，定义域 ．
时，y=a3，并且技术改造投入满足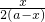
∈（0，t]，其中t为常数且t∈（1，2]．