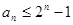摘要:已知为正实数,数列由,确定. (Ⅰ)对于一切的,证明:, (Ⅱ)若是满足的正实数,且,证明:.
网址:http://m.1010jiajiao.com/timu3_id_517384[举报]
(本小题满分12分)
已知数列 和
和 满足:
满足: ,
, 其中
其中 为实数,
为实数, 为正整数.
为正整数.
(1)对任意实数 ,证明数列
,证明数列 不是等比数列;
不是等比数列;
(2)试判断数列 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(3)设 ,
, 为数列
为数列 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看习题详情和答案>>
(本小题满分12分)
已知数列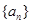 和
和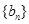 满足:
满足: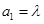 ,
,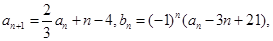 其中
其中 为实数,
为实数,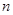 为正整数.
为正整数.
(1)对任意实数 ,证明数列
,证明数列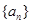 不是等比数列;
不是等比数列;
(2)试判断数列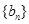 是否为等比数列,并证明你的结论;
是否为等比数列,并证明你的结论;
(3)设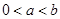 ,
,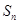 为数列
为数列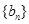 的前
的前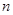 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数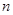 ,都有
,都有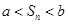 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本小题满分12分)
已知函数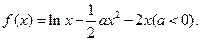
(1)若函数 在定义域内单调递增,求
在定义域内单调递增,求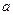 的取值范围;
的取值范围;
(2)若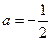 且关于x的方程
且关于x的方程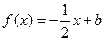 在
在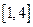 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数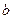 的取值范围;
的取值范围;
(3)设各项为正的数列 满足:
满足: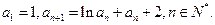 求证:
求证: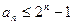
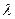 ,an+1=
,an+1=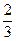 an+n-4,bn=(-1)n(an-3n+21),其中
an+n-4,bn=(-1)n(an-3n+21),其中 任意实数
任意实数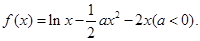
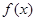 在定义域内单调递增,求
在定义域内单调递增,求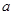 的取值范围;
的取值范围; 且关于x的方程
且关于x的方程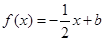 在
在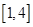 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数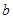 的取值范围;
的取值范围;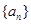 满足:
满足: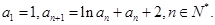 求证:
求证: