摘要:6.已知常数.经过定点A以(l.a)为方向向量的直线与经过定点B(0.a)以(1.-2la)为方向向量的直线相交于点P.其中试问:是否存在两个定点E.F.使得|PE|+|PF|为定值.若存在.求出E.F的坐标,若不存在.说明理由. 解:根据题设条件.首先求出点P坐标满足的方程.据此再判断是否存在两定点.使得点P到两定点距离的和为定值. 因此.直线AP和BP的方程为 l(y+a)=ax 和 y-a=-2lax. 消去参数l.得点P(x.y)的坐标满足方程y2-a2=-2a2x2. 整理得 . ① 因为a>0.所以得: (ⅰ)当时.方程①是圆方程.故不存在合乎题意的定点E和F, (ⅱ)当时.方程①表示椭圆.焦点和为合乎题意的两个定点: (ⅲ)当时.方程①也表示椭圆.焦点和为合乎题意的两个定点.
网址:http://m.1010jiajiao.com/timu3_id_516848[举报]
已知常数a>0,向量
=(0,a),
=(1,0)经过定点A(0,-a)以
+λ
为方向向量的直线与经过定点B(0,a)以
+2λ
为方向向量的直线相交于点P,其中λ∈R.
(I)求点P的轨迹C的方程;
(Ⅱ)若a=
,过E(0,1)的直线l交曲线C于M、N两点,求
•
的取值范围.
查看习题详情和答案>>
| m |
| n |
| m |
| n |
| n |
| m |
(I)求点P的轨迹C的方程;
(Ⅱ)若a=
| ||
| 2 |
| EM |
| EN |
已知常数a>0,向量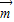 =(0,a),
=(0,a),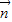 =(1,0)经过定点A(0,-a)以
=(1,0)经过定点A(0,-a)以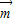 +
+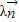 为方向向量的直线与经过定点B(0,a)以
为方向向量的直线与经过定点B(0,a)以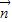 +2
+2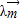 为方向向量的直线相交于点P,其中λ∈R.
为方向向量的直线相交于点P,其中λ∈R.
(I)求点P的轨迹C的方程;
(Ⅱ)若a=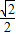 ,过E(0,1)的直线l交曲线C于M、N两点,求
,过E(0,1)的直线l交曲线C于M、N两点,求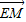 •
•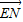 的取值范围.
的取值范围.
查看习题详情和答案>>
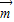 =(0,a),
=(0,a),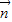 =(1,0)经过定点A(0,-a)以
=(1,0)经过定点A(0,-a)以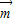 +
+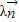 为方向向量的直线与经过定点B(0,a)以
为方向向量的直线与经过定点B(0,a)以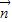 +2
+2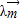 为方向向量的直线相交于点P,其中λ∈R.
为方向向量的直线相交于点P,其中λ∈R.(I)求点P的轨迹C的方程;
(Ⅱ)若a=
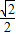 ,过E(0,1)的直线l交曲线C于M、N两点,求
,过E(0,1)的直线l交曲线C于M、N两点,求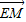 •
•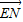 的取值范围.
的取值范围.查看习题详情和答案>>
已知常数a0,向量c0,a,i1,0,经过原点O以cli为方向向量的直线与经过定点A0,a以i